When is the bottom of a Pint Glass exposed?

Considering the task as 2-dimensional problem via a cut of the cone with a plane containing the rotation axis I took into account that the area of the trapezium filled with beer when the glass stands uprightly must be equal the area of the triangle formed by the lower left, lower right and upper right point of the trapezium representing the glass.

I got a non-linaer equations' system for whole height of the cone e, height of glass h, top diameter of glass b, lower diameter of glass a and diameter of beer level t. z denotes the ratio to be determined:

e=b*h/(b-a)

t=(7 b+9 a)/16

a/2 (e-h) (sqrt((b^2+4 e^2)/(a^2+4 (e-h)^2))-1)=h (a+t)/2 7/16

473,2=pi/12 (b^2 e-a^2*(e-h))

t/b=(e-9/16*h)/e

z=h/e

A possible solution vector is:

Lösung im 4. Durchlauf nach 10 Iterationen gefunden:

z = 0,3950617284 e = 5,881211333621 b = 19,86740500848 h = 2,323441514547 a = 12,01855364702 t = 15,452426117691

For any other solution vectors the ratio z remains constant.As last step I converted the ratio into the proper form as a rational number finally to get the solution $\boxed{113}$ .

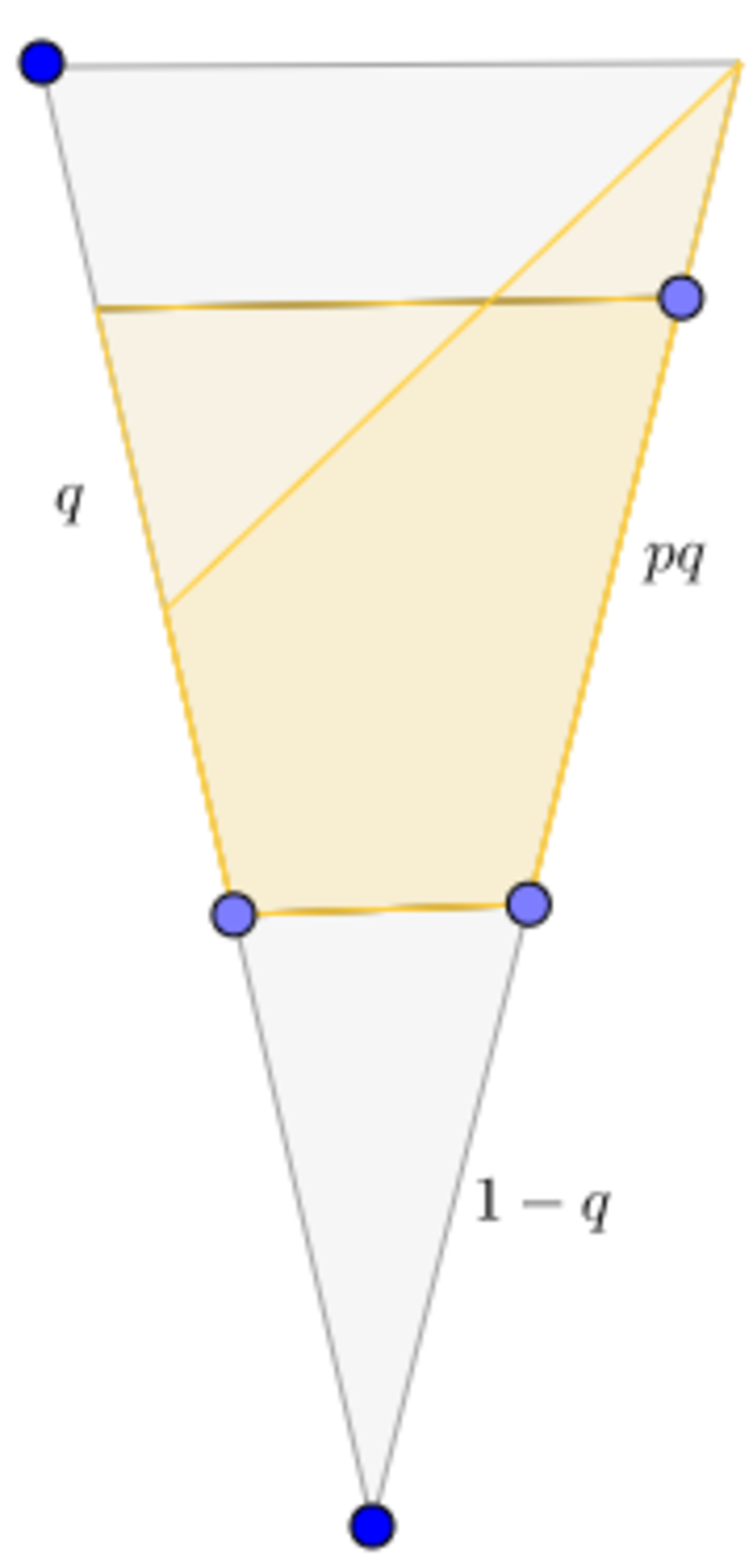WLOG, give the associated cone convenient dimensions: side length 1. Then, because in general liquid that reaches $x$ of the way up the side in an upright conic vessel reaches $x^2$ up the opposite side when tipped to the point of spilling (see proof below):

$1-q=(pq+(1-q))^2=p^2q^2+q^2+1+2pq-2pq^2-2q$

Solving,

$q = 1-(\frac{p}{1-p})^2$

For $p = \frac{7}{16}$ , $q=\frac{32}{81}$ . So our answer is $\boxed{113}$

Proof of squaring fact:

Side-view of conical vessel, such as a martini glass.

Assume without loss of generality that the side-length of the glass is $1$ and the apex a right angle, with $x$ and $y$ axes along sides of the glass as in the diagram, and consider the simple squeeze mapping $M$ :

$M=\left(\begin{matrix} \frac{1}{k} & 0 & 0 \\ 0 & k & 0 \\ 0 & 0 & 1 \end{matrix} \right)$

For those unfamiliar with the matrix representation, $M$ represents a function, an affine linear transformation, that maps coordinates to coordinates as follows: $(x',y',z') = (\frac{x}{k},ky,z)$ We will now show that $M$ maps (the coordinates in) the upright liquid cone to (the coordinates in) an oblique elliptical cone that also is bounded by the cone of the glass. The planar surface of the upright liquid (the steeper blue line) is mapped to another planar surface (the shallower one). Like every point on the cone, each of the original perimeter points either is on the $x$ or $y$ axes and stays there under transformation, or is on a cross-section of the glass cone that follows a hyperbola of the form (for some particular $z$ ) $xy=\frac{z^2}{2}$ , and stays on that hyperbola under transformation (because $x'y'=xy$ ), and hence stays on the cone. So $M$ maps the perimeter to a co-planar closed curve on the cone: an ellipse. When $k=p$ , an $x$ value of $p$ maps to $1$ , so the highest point on the ellipse is at the rim. Squeeze mappings are volume-preserving (see below). Thus with $k=p$ we have the cone we are looking for: same volume, perimeter of the base on the glass cone, and tipped to the rim. And $y=p$ maps to $y'=p^2$ , so the lower edge of the elliptical surface is $p^2$ of the way up the side. Therefore the answer is $p^2$ (indeed the product of the side-lengths of the liquid cone is $p^2$ for any value of $k$ ).

(To see that $M$ preserves area in the $x-y$ plane, consider any figure broken up into infinitesimal squares of side $s$ and area $s^2$ , oriented with the axes. $M$ maps these to rectangles of sides $\frac{s}{k}$ and $sk$ , and so they retain their area. That volume is preserved follows easily, since depth ( $z$ ) is unchanged.)

The convenient dimensions are WLOG because any cone can be obtained from ours by uniform scaling in height (to get the shape) and three dimensional scaling (to get the size), neither of which affects the ratios of volumes (liquid to cone) and lengths we are concerned with.