A geometry problem by A Former Brilliant Member
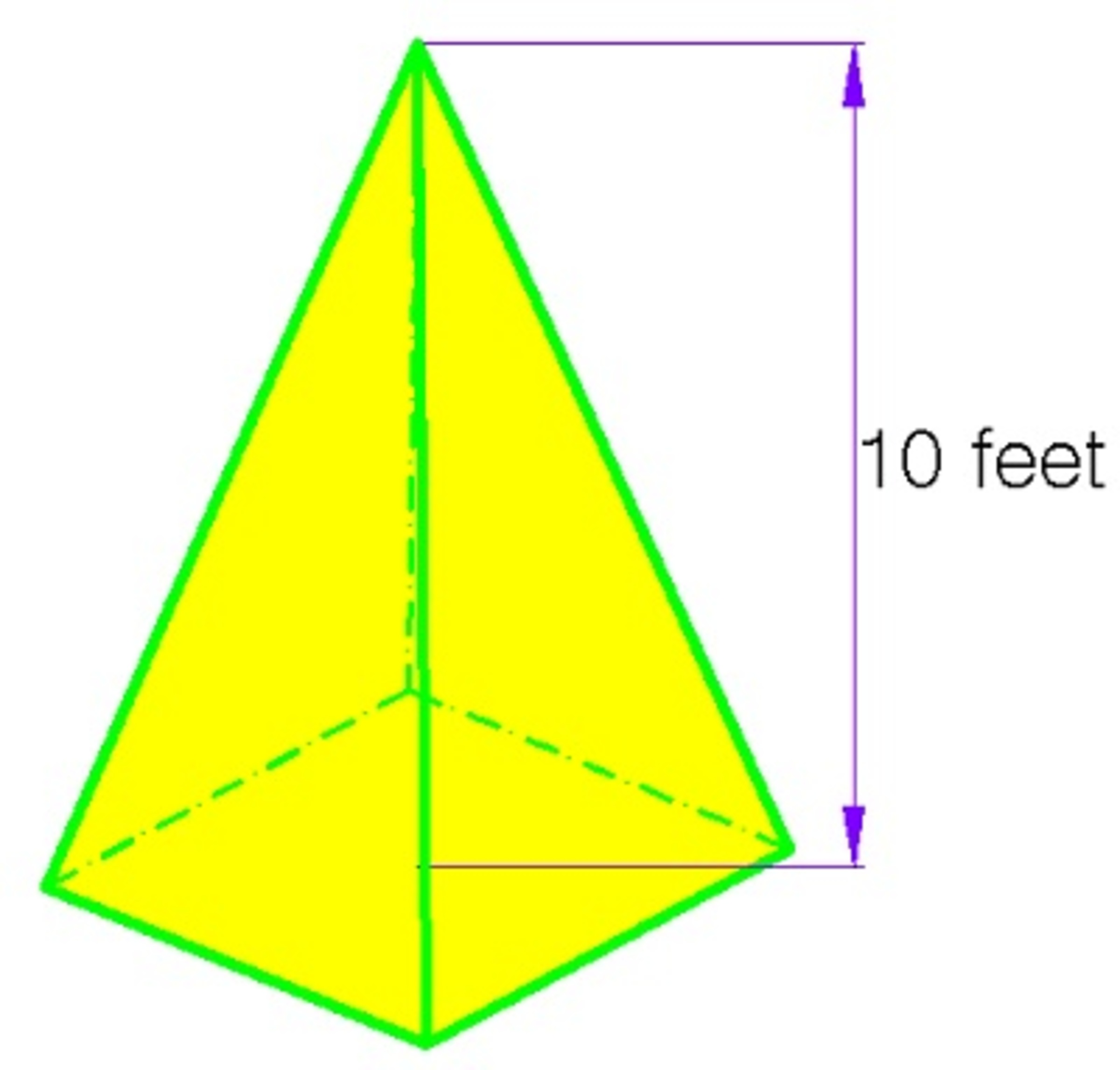 A regular square pyramid has a height of 10 feet and weighs 900 pounds. At what distance
from its base must be cut by a plane parallel to its base such that the two cuts will be of equal weights?
A regular square pyramid has a height of 10 feet and weighs 900 pounds. At what distance
from its base must be cut by a plane parallel to its base such that the two cuts will be of equal weights?
Round your answer to 2 decimal places.
The answer is 2.06.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
V 9 0 0 = V 1 4 5 0 ⟹ V V 1 = 2 1
We know that the volume of similar solids ( V 1 , V ) have the same ratio as the cubes of any two corresponding lines. So
V V 1 = 1 0 3 x 3
Equating V V 1 = V V 1 , we have
2 1 = 1 0 3 x 3
x = 7 . 9 3 7 0 0 5 2 6
Finally,
y = 1 0 − x = 2 . 0 6 f e e t