A geometry problem by A Former Brilliant Member
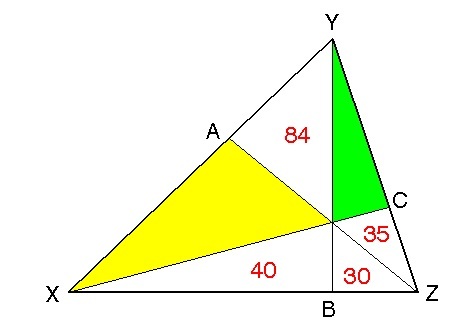 A triangle is divided by three lines to form
6
small triangles as shown above. The areas of some triangles are given.What is the ratio of the area of the yellow region to the area of the green region?
A triangle is divided by three lines to form
6
small triangles as shown above. The areas of some triangles are given.What is the ratio of the area of the yellow region to the area of the green region?
The answer is 0.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
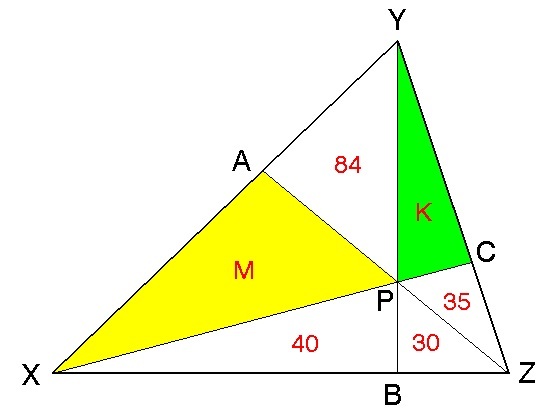 Let
M
be the area of the yellow region and
K
be the area of the green region. Note that triangle
X
P
B
and triangle
Z
P
B
share the same altitude from
P
, so the ratio of their areas is the same as the ratio of their bases. Similarly, triangle
X
Y
B
and triangle
Z
Y
B
share the same altitude from
Y
, so the ratio of their areas is the same as the ratio of their bases. Moreover, the two pairs of bases are actually the same, and thus in the same ratio. As a result, we have:
Let
M
be the area of the yellow region and
K
be the area of the green region. Note that triangle
X
P
B
and triangle
Z
P
B
share the same altitude from
P
, so the ratio of their areas is the same as the ratio of their bases. Similarly, triangle
X
Y
B
and triangle
Z
Y
B
share the same altitude from
Y
, so the ratio of their areas is the same as the ratio of their bases. Moreover, the two pairs of bases are actually the same, and thus in the same ratio. As a result, we have:
3 0 4 0 = 6 5 + K 1 2 4 + M ⟹ 4 K = 3 M + 1 1 2
Applying identical reasoning to the triangles with bases Y C and Z C , we get
3 5 K = 1 0 5 M + K + 8 4 ⟹ 2 K = M + 8 4
Substituting from this equation into the previous one gives M = 5 6 , from which we get K = 7 0 .
Finally,
K M = 7 0 5 6 = 0 . 8 .
M + 4 0 + 3 0 3 5 + 8 4 + K = M 8 4
M + 7 0 1 1 9 + K = M 8 4
1 1 9 M + M K = 8 4 ( M + 7 0 )
3 5 M + M K = 5 8 8 0 ( 1 )
3 0 + 3 5 + K 8 4 + 4 0 + M = 3 0 4 0
( 1 2 4 + M ) ( 3 0 ) = 4 0 ( 6 5 + K )
3 7 2 0 + 3 0 M = 2 6 0 0 + 4 0 K
1 1 2 + 3 M = 4 K
K = 4 1 1 2 + 3 M = 2 8 + 4 3 M ( 2 )
Substitute ( 2 ) in ( 1 ) .
3 5 M + M ( 2 8 + 4 3 M ) = 5 8 8 0
3 5 M + 2 8 M + 4 3 M 2 = 5 8 8 0
4 3 M 2 + 6 3 M − 5 8 8 0 = 0
M = 5 6
It follows that
B = 2 8 + 4 3 ( 5 6 ) = 7 0
The desired answer is 7 0 5 6 = 0 . 8