Volume of a solid

The lowest two steps can be put on top of the upper steps as shown, making a rectangular solid with dimensions $w=7\times 12, l=6\times 12+11\times 2, h=7\times 5$ . The volume is then the product of all of these:

$V=84\times94\times35=\boxed{276,360}$

The volume considered from the lowest step:

$\begin{aligned} V & = (7 \times 12)(11(7+14+21+28) +(6\times 12)(35)) \\ & = 84(11(70)+72(35)) \\ & = \boxed{276360} \end{aligned}$

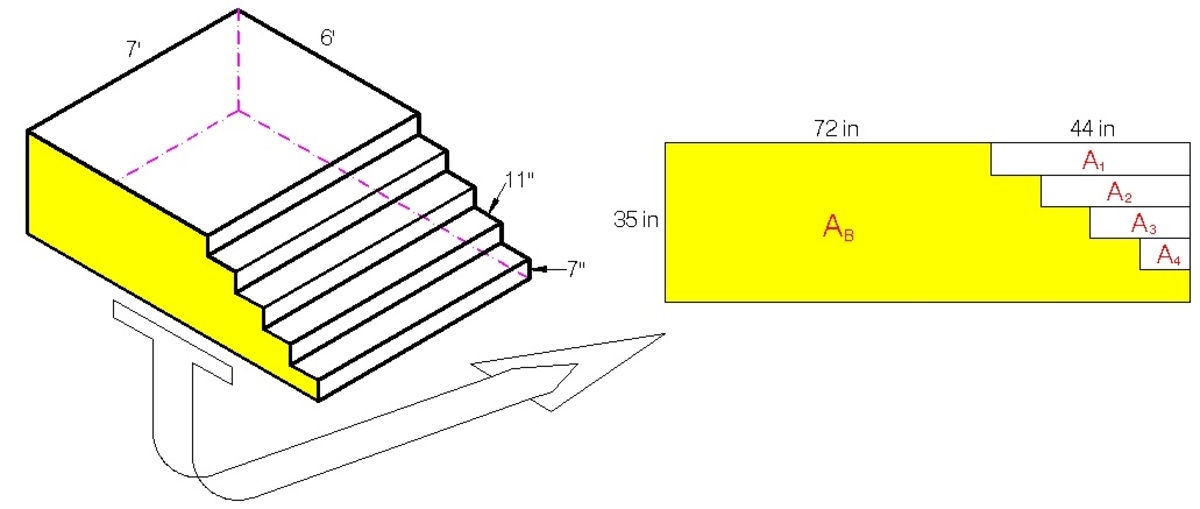This can be analyzed as right prism letting the yellow region as the base. Convert all feet to inches. $V=A_bL$ where: $A_b$ = area of the base and $L$ = length of each step and landing

$A_b=A_{rectangle}-A_1-A_2-A_3-A_4=[(35)(72+44)]-(44)(7)-(33)(7)-(22)(7)-(11)(7)=4060-308-231-154-77=3290$

Finally,

$V=3290(84)=276360~in^3$ $\boxed{\text{answer}}$