A geometry problem by A Former Brilliant Member
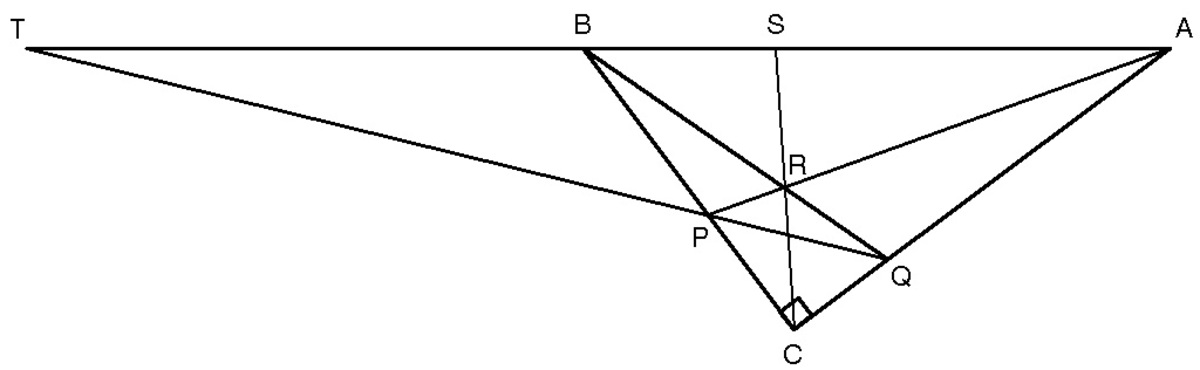 In right
△
A
B
C
,
P
and
Q
are on
B
C
and
A
C
, respectively, such that
C
P
=
C
Q
=
5
. A line is drawn from
C
passing through the intersection of
A
P
and
B
Q
and meeting
A
B
at
S
.
In right
△
A
B
C
,
P
and
Q
are on
B
C
and
A
C
, respectively, such that
C
P
=
C
Q
=
5
. A line is drawn from
C
passing through the intersection of
A
P
and
B
Q
and meeting
A
B
at
S
.
Q P is extended so that it meets A B at T . If A B = 2 5 and A C = 2 0 , find T S .
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I used Menelaus' Theorem on four triangles after naming intersection of CS and PQ as V.
Δ
s
a
n
d
t
r
a
n
s
v
e
r
s
a
l
s
:
−
B
S
C
w
i
t
h
T
P
V
,
a
n
d
S
A
C
w
i
t
h
T
V
Q
a
n
d
g
o
t
A
T
/
T
B
=
1
5
/
1
0
B
S
C
w
i
t
h
P
R
A
,
a
n
d
S
A
C
w
i
t
h
B
R
Q
a
n
d
g
o
t
B
S
/
A
S
=
1
0
/
1
5
A
n
d
u
s
e
d
c
o
m
p
o
n
e
n
d
o
−
d
i
v
i
d
e
n
d
o
t
o
o
b
t
a
i
n
T
B
=
5
0
a
n
d
B
S
=
1
0
.
T
S
=
6
0
.
Brilliant Member's solution is a better one.
B C 2 = 2 5 2 − 2 0 2 ⟹ B C 2 = 2 2 5 ⟹ B C = 2 2 5 ⟹ B C = 1 5
It follows that, B P = 1 5 − 5 = 1 0 .
In △ A B C , since A P , B Q and C S are concurrent, we have
Q C A Q × P B C P × S A B S = 1 ( Ceva's Theorem )
Substituting, we have
5 1 5 × 1 0 5 × 2 5 − B S B S = 1 ⟹ B S = 1 0
Now, consider △ A B C with transversal Q P T .
Q C A Q × P B C P × T A B T = − 1 ( Menelaus' Theorem )
Since we are not dealing with directed line segments, this may be restated as
( A Q ) ( C P ) ( B T ) = ( Q C ) ( P B ) ( A T )
Substituting, we have
( 1 5 ) ( 5 ) ( B T ) = ( 5 ) ( 1 0 ) ( B + 2 5 ) ⟹ B T = 5 0
Finally, T S = B T + B S = 5 0 + 1 0 = 6 0 answer