A geometry problem by A Former Brilliant Member
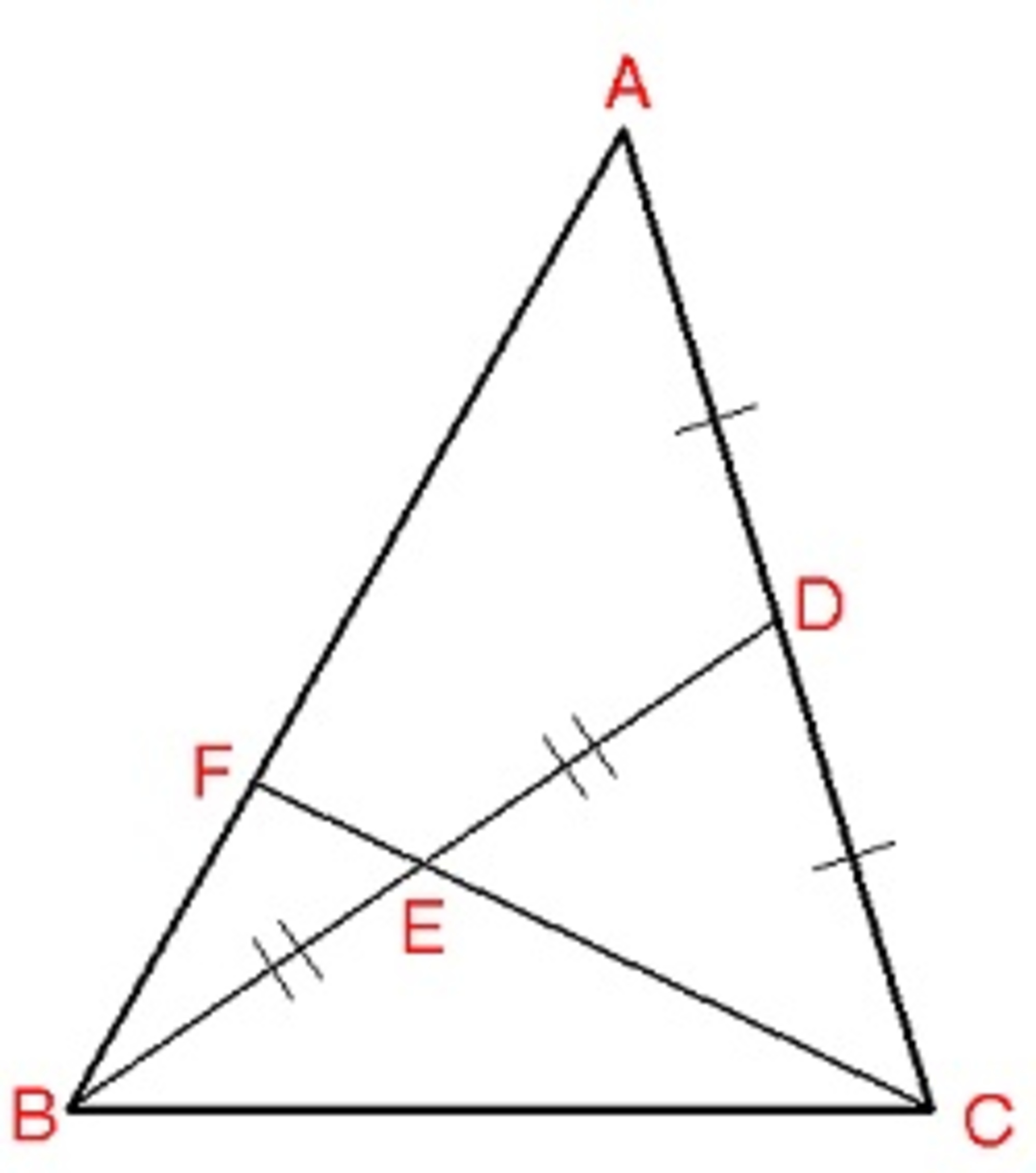 In the triangle shown above,
is a median. Point
is the midpoint of
. Line
extended meets
at
. If
, find
.
In the triangle shown above,
is a median. Point
is the midpoint of
. Line
extended meets
at
. If
, find
.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let F B = x and apply Menelaus' Theorem to △ A B D with transversal C F :
F B A F × E D B E × C A D C = − 1
which implies that,
x A F × 1 × ( − 2 1 ) = − 1
A F = 2 x , so A B = 3 x , and it follows that
x = 3 A B = 3 6 = 2