A geometry problem by Mehul Chaturvedi
Geometry
Level
4
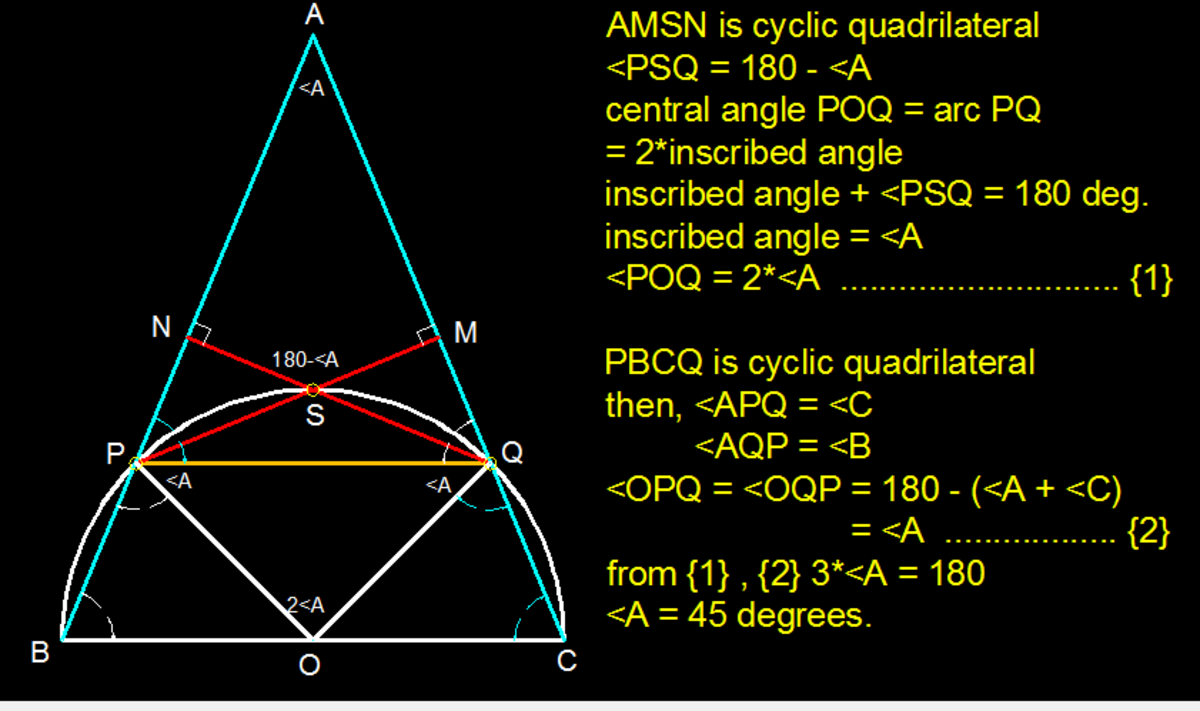
Let ABC be an acute-angled triangle. The circle I' with BC as diameter intersects AB and AC again at P and Q, respectively. Determine ∠BAC given that the orthocentre of triangleAP Q lies on I'.
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Due to symmetry, △ A B C is an isosceles triangle with A B = A C . Let the coordinates be O ( 0 , 0 ) , A ( 0 , a ) , B ( − 1 , 0 ) and C ( 1 , 0 ) .
The straight line A C is given by:
x − 1 y − 0 = 0 − 1 a − 0 ⇒ y = a ( 1 − x ) . . . ( 1 )
Straight line B Q is given by:
x + 1 y − 0 = b 1 ⇒ y = a 1 + x . . . ( 2 )
Therefore the coordinates of Q are:
y Q = a ( 1 − x Q ) = a 1 + x Q ⇒ x Q = a 2 + 1 a 2 − 1 ⇒ y Q = a 2 + 1 2 a
Let the heights of the orthocenter of △ A B C and △ A P Q be h and h ′ respectively. Then we note that:
a 2 + 1 a 2 − 1 h ′ = 1 h = a 1 ⇒ a 2 + 1 a 2 − 1 1 − a 2 + 1 2 a = a 1 ⇒ a ( a − 1 ) 2 = a 2 − 1
⇒ a ( a − 1 ) = a + 1 ⇒ a 2 − 2 a − 1 = 0 ⇒ a = 1 + 2
We note that ∠ B A C = 2 tan − 1 a 1 = 2 tan − 1 ( 2 − 1 ) = 4 5 ∘