Congruent Circles Intersection
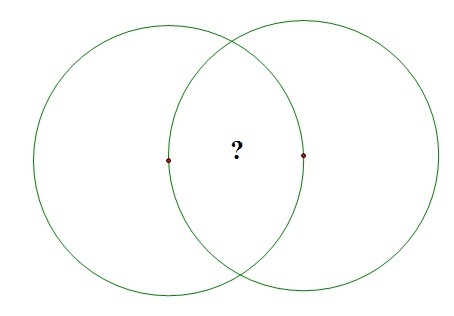 The above diagram shows 2 congruent circles of radius 6, and each circle passes through the center of the other circle.
The above diagram shows 2 congruent circles of radius 6, and each circle passes through the center of the other circle.
To the nearest whole number, what is the area common to the two circles?
The answer is 44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
can u pls explain it clearly
Log in to reply
He used the formula to find the area of a minor segment that is part of the common area from each circle, which is 1/2 r^2 (θ-sinθ). The minor segments can be found if you simply slice the common area into 2, which is why he wrote the formula as (θ-sinθ) r^2, to include both segments because
1/2r^2 (θ-sinθ)×2
=r^2 (θ-sinθ)
Then, to find θ, within the common area, the equal radii lengths forms 2 equilateral triangles, so θ=120° converted to radians is 2π /3
When that is substituted into the earlier equation, we get
(θ-sinθ) r^2
=( 2π/3-sin( 2π/3) ) ×6^2
=(1.228) ×36
= 44.22
So, from the equation, we can find the approximate common area to be 44.
Join all the points inside area covered b/w two circles and make a Rhombus.
Area covered by 2 congruent circles= (2* area of a sector)-area of Rhombus = 24 * 3.141-18 * 1.732 =44.208
Area common to 2 circles can be divided into 2 by a vertical line passing through the 2 points of intersection. Area of each half is the area of the sector from centre minus the area of triangle including the vertical chord. Area of sector is 1/2 r^2 angle in radians. Area of triangle is 1/2 * length of chord * distance of chord from centre Distance of chord from centre is r/2, hence length of chord is sqrt(3)*r.
nice solution sir
Very nice Sir...
Draw a line between the centers, between the 2 intersection points, and between the centers and the intersection points. Four right triangles are formed by the symmetry, each with sides 3, 6, 3 squareroot(3). Those are clearly 30-60-90 right triangles, so the angle of the two radii lines from each center is 120 degrees -- which subtends 1/3 the area of one circle. That's 1/3 * pi * r^2 = 12 * pi, which is approximately 37.68. The area of the triangular part that is subtended is 1/2bh = 3 squareroot(3) * 3 = 9*squareroot(3), which is approximately 15.57. To find 1/2 the area of the common area, just subtract the area of the triangle formed from the area subtended by the 2 radii, which is 37.68-15.57 = 22.11. Since there are 2 of these to form the common area, the total is approximately 44.
My favorite of all the solutions. Very nicely done.
I did it without trigonometry. Each circular area was the union of a hexagon and a set of circular "slivers", each hexagon was the union of six disjoint triangles, and the intersection was two such triangles and four "slivers".
The triangles can be found with the Pythagorean Theorem, the hexagon is six triangles, the six slivers are the difference, one sliver is a sixth of it, and then you just have to put the pieces together.
Right, but what is the area of the sliver?
Log in to reply
The area of the sliver is 6 A c i r c l e − A h e x a g o n
The area of the circle is π r 2 = 3 6 π
The hexagon is made up of six equilateral triangles of side length 6
b = 6
h = 3 3
2 b h = 2 6 × 3 3 = 9 3
A h e x a g o n = 6 ( 9 3 ) = 5 4 3
A s l i v e r = 6 3 6 π − 5 4 3 ≈ 3 . 2 6
Simple and elegant. I much prefer this type of solution to those using "derived formulas",
Calculus based solution:
Note: In order to save space, I've omitted all simplification and integral evaluation steps; the simplification steps are pretty straight forward, but the integration evaluations rely on integrating functions of the form: f ( x ) = a 2 − x 2
The integral of this type of function can be found in a table of integrals.
Now, lets get started:
We can create an equation to represent each of the circles:
x 2 + y 2 = r 2 and ( x − r ) 2 + y 2 = r 2
Solving each equation for y yields: y = ± r 2 − x 2 and y = ± r 2 − ( x − r ) 2
We will only need the equation of one half of each circle (since circles are symmetrical), so we will ignore the negative square roots.
Let B be the area of a quarter of a circle therefore:
B = ∫ 0 r r 2 − ( x − r ) 2 d x = 4 π r 2 as expected
Let B ′ be the area of the part of that quarter that is not being shared with the other circle ( r / 2 is the upper bound of the integral because that is the x-coordinate of the points where the circles intersect):
B ′ = ∫ 0 r / 2 ( r 2 − x 2 − r 2 − ( x − r ) 2 ) d x
Which simplifies to a very nice expression:
B ′ = 1 2 r 2 ( 3 3 − π )
Now let A be the shared area of both circles, we see that: A = 2 ( B − B ′ )
Substituting the expressions for B and B ′ into the formula for A and simplifying yields:
A = 6 r 2 ( 4 π − 3 3 )
Substituting the given value of r , in this case r = 6 , yields:
A = 2 4 π − 1 8 3
A ≈ 4 4
I did it similarly to this, but turned sideways. Took 3 flippin pages. Should have noticed the sector and triangle method :P
nice. I like this site because you can see all the different ways of solving a solution.
1) Join the two centers of the circle (say 'm'). Also, join the 2 points where the circles intersect (this is a chord, say 'n'). Join these 4 points to form a quadrilateral. The quadrilateral has all its sides = 6. Also, 'm' = 6. 2) The two triangles formed here (w.r.t. the 2 centers and intersection of the circle) are 2 equilateral triangles. The chord 'n' cuts line segment 'm' at 90 degrees (s̲i̲n̲c̲e̲,̲ ̲i̲n̲ ̲a̲n̲ ̲e̲q̲u̲i̲l̲a̲t̲e̲r̲a̲l̲ ̲t̲r̲i̲a̲n̲g̲l̲e̲; ̲p̲e̲r̲p̲e̲n̲d̲i̲c̲u̲l̲a̲r̲ ̲b̲i̲s̲e̲c̲t̲o̲r̲, e̲a̲c̲h̲ ̲a̲l̲t̲i̲t̲u̲d̲e̲,̲ ̲m̲e̲d̲i̲a̲n̲ ̲a̲n̲d̲ ̲a̲n̲g̲l̲e̲ ̲b̲i̲s̲e̲c̲t̲o̲r̲ ̲d̲r̲a̲w̲n̲ ̲f̲r̲o̲m̲ ̲t̲h̲e̲ ̲s̲a̲m̲e̲ ̲v̲e̲r̲t̲e̲x̲,̲ o̲v̲e̲r̲l̲a̲p̲). Thus, 'm', and 'n' divides the quadrilateral into 4 triangles of 30-60-90 degrees each. 3) The area of the portion asked in the question = area of the quadrilateral + area of the 4 remaining small segments. 4) Area of the quadrilateral = area of the 4 right angled triangles = 4 (1/2) (3) (3 sqrt(3)) = 18 sqrt(3), (By Pythagorean theorem: the altitude of the right angled triangle = sqrt(6^2-3^2) = 3 sqrt(3)). 5) The area of 2 of the small segments = Area of sector - area of quadrilateral. Area of sector is given by: (pi r^2 angle)/360 degrees = (pi 6^2 120)/360 = 12 pi. Therefore, area of the 2 small segments = 12 pi - 18 sqrt(3). Total area of the 4 small segments = 2 (12 pi-18 sqrt(3)) = (24 pi - 36 sqrt(3)). 6) Thus, the area of the portion is given by, 18 sqrt(3) + (24 pi - 36*sqrt(3)) = 44.22130915 ~ 44.
The area to be found can be vertically bisected to form two circular segments, each with area 2 1 ( θ − sin θ ) r 2 .
This is because the area of a circular sector of angle θ is 2 1 θ r 2 , and the area of the triangle formed by the centre of the circle and the two points of the sector's arc is 2 1 r 2 sin θ .
The total area to be found is thus ( θ − sin θ ) r 2 , where θ is to be found.
If a triangle is formed between the two centres and one of the intersections, it can easily be seen that an equilateral triangle is formed. Thus, θ = 3 2 π . This is substituted into the equation, along with r = 6, and the area is thus found to be 44.2 square units, or approximately 44 square units.