A geometry problem by Mohammad Arman Khaled
Geometry
Level
1
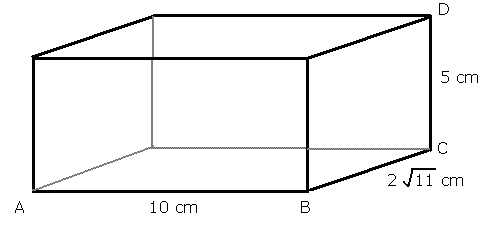A cuboid has sides of length 10cm, 2 √11 cm and 5cm. Find the length of a diagonal.
(Please refer the given diagram for your convenience!)
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
So we want to find the diagonal..... let it be diagonal AD. (it can be the other diagonals too ).
We can draw a right-angled triangle inside the cuboid which has AD as it's hypotenuse.
Then we can use Pythagoras.
A right-angled triangle with AD as it's hypotenuse
To use Pythagoras, we need to know AC and CD. We know that CD is 5 cm. We need to find AC.
We can use Pythagoras to find AC, because if we look at the cuboid from above, we see that AC is the diagonal of a rectangle
AC is the diagonal of a rectangle
ABC is a right angled triangle, so by Pythagoras, AC^2 = AB^2 + BC^2 = 102 + (2 √11)2 = 100 + 44 = 144
Now we can find AD: AD^2 = AC^2 + CD^2 = 144 + 25 = 169
Therefore AD = square root of 169 which is 13 SO the diagonal is 13 cm. hope the answer is quite easy. Thanks for approaching my answer!