Confusing square
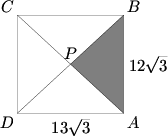 The rectangle
below has dimensions
and
. Diagonals
and
intersect at
. If triangle
is cut out and removed, edges
and
are joined, and the figure is then creased along segments
and
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
The rectangle
below has dimensions
and
. Diagonals
and
intersect at
. If triangle
is cut out and removed, edges
and
are joined, and the figure is then creased along segments
and
, we obtain a triangular pyramid, all four of whose faces are isosceles triangles. Find the volume of this pyramid.
The answer is 594.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The outer edge B C D A will form an isoscelese triangle. Let put it in the xy-plane, such that its axis of symmetry coincides with the y-axis, and its base C D with the x-axis. It has vertices with these coordinates:
A and B will be at v 3 = ( 0 , y 3 , 0 )
By symmetry, the 4th vertex v 4 must lie in the y z -plane, so
P will be at v 4 = ( 0 , y 4 , z 4 ) .
Since d ( A , D ) = 1 3 3 = ∣ v 3 − v 1 ∣ = ∣ ( 6 3 , y 3 , 0 ) ∣ = 1 0 8 + y 3 2 we infer that y 3 = ± 3 9 9 . Let's choose the positive one: y 3 = 3 9 9
v 4 is equidistant to each of the other vertices. This distance (let's name it d ) is half a diagonal in the original plan, which is d = 2 1 ( 1 3 3 ) 2 + ( 1 2 3 ) 2 = 2 1 9 3 9
Now express the squared distance to each other vertex as d 1 4 2 = d 2 4 2 = 1 0 8 + y 4 2 + z 4 2 = d 2 d 3 4 2 = ( y 4 − y 3 ) 2 + z 4 2 = d 2
Setting these equal we get 1 0 8 + y 4 2 − ( y 4 − y 3 ) 2 = 0 , which simplifies to y 4 = y 3 / 2 − 5 4 / y 3 . Using the known value for y 3 we get y 4 = 7 9 8 2 9 1 3 9 9
Finally, using z 4 2 = d 2 − ( y 4 − y 3 ) 2 and filling in the known values, we find z 4 = 1 3 3 9 9
Numerically we have the following approximations, which makes it easier to check for mistakes:
v 1 = ( − 1 0 . 3 9 , 0 , 0 ) , v 2 = ( 1 0 . 3 9 , 0 , 0 ) , v 3 = ( 0 , 1 9 . 9 7 , 0 ) , v 4 = ( 0 , 7 . 2 8 4 , 8 . 5 8 4 )
d 1 2 = 2 0 . 7 8 , d 1 3 = d 2 3 = 2 2 . 5 2 , d 1 4 = d 2 4 = 1 5 . 3 2 , d 3 4 = 1 5 . 3 2
The volume of the piramid is given by V = 3 1 A h = 3 1 x 2 y 3 z 4 = 3 1 6 3 3 9 9 1 3 3 9 9 V = 5 9 4