A geometry problem by Muhammad Fahad Khan
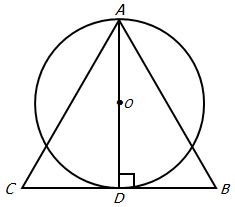 If the circle with center O has area
9
π
, what is area of equilateral triangle ABC?
If the circle with center O has area
9
π
, what is area of equilateral triangle ABC?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Finally a smart person in here
Since the circle has area 9 π , we know that the radius is 3, which implies that the height of the equilateral triangle is 6. This implies that C D = 3 6 . Thus the area is just 6 ( 3 6 ) ≈ 2 0 . 7 8 4
Can you add a few lines explaining how you arrived at that calculation?
Log in to reply
I have added the lines.
the height of the triangle is 6 and since it is an equilateral triangle, the rest comes from elementary geometry. The area = 12*sqrt[3].
Area = 9(pi)
AD =dia = 6
CD = AC/2 = (AC^2 - 6^2)^(1/2)
AC = (48)^(1/2)
Area of triangle = 1/2 * b * h = 1/2 * 6.9282 * 6 = 20.7846(Ans.)
As circles area is 9 π = r 2 π ⇒ the circle's radii is 3 ⇒ A D = 6 .
Then, sin 6 0 ° A D = sin 9 0 A B ⇒ 2 3 6 = 1 A B ∴ A B = 3 1 2 = 4 3
Finally, the area of A B C is 2 4 3 × 6 = 1 2 3
area of circle=9 pi by area of circle=9pi radius=3 In triangle ACD, Sin60=6/AC (as radius=3, diameter=6) AC=12/root3, area of equilateral triangle= root3/4 length^2 12 root 3 is the answer,
Sorry for not being able to type root 3....this ws my first time typing any answer like this...