A geometry problem by Neil Patram

There are many ways to arrive at the answer; the one I saw at first was more complicated, but a friend of mine pointed out a more clever way to solve it. I will present both ways.

Way 1: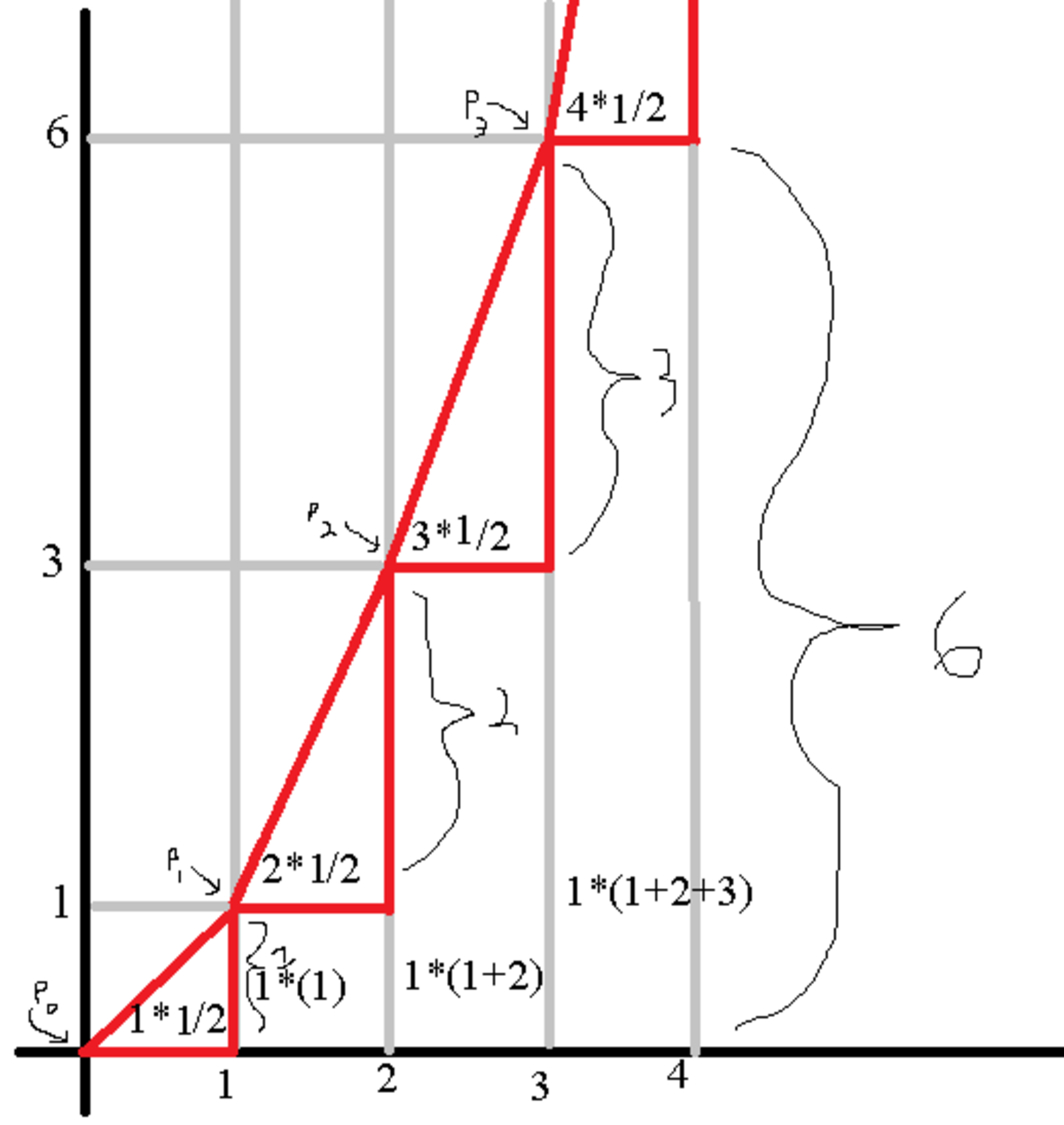

Draw triangles inside the shape as shown in the (very high-quality) diagram. Let's consider what would happen if we were considering the line $x = 0$ instead of $x = 2017$ . Obviously, the answer would be $0$ . For $x = 1$ , the answer would be $\frac{1*1}{2}$ . However, after that, the addition starts to get a little complicated, but in the diagram, you can see that a rectangle has area $1+2+3+...+n$ if it is between the lines $x=n$ and $x=(n+1)$ . (A visual way of representing this is to move all of the triangles right so that their legs make a straight line. That line will have length $1+2+3+...+n$ .) This sum can also be represented as $\binom{n}{1}$ . This notation makes everything a lot easier to add.

As for the triangles, they will have area $\frac{n}{2}$ (by the definition of the area of a triangle).

So we have two different shapes we're dealing with: rectangles and triangles. The sum of all the rectangles should be $\displaystyle \sum_{x=1}^{2017} {\binom{n}{2}}$ , which, by the Hockey Stick Theorem, is equal to $\binom{2018}{3}$ .

The area of all the triangles is $\displaystyle \sum_{x=1}^{2017} {\frac{n}{2}}$ , which is equal to the half of sum of the numbers from 1 to 2017. This is equal to $\frac{1}{2} * \binom{2018}{2}$ .

Since we want to find the last three digits of twice the area, we can go ahead and multiply by 2, then take the last three digits.

$\binom{2018}{2}\ + 2\binom{2018}{3} = \frac{2018*2017}{2}*\frac{2*2018*2017*2016}{6}\ = 2035153+2735245632\ = 2737280785$

So the answer is 785

Way 2: This is the other (much simpler) method that I didn't see at first. Instead of finding the area of the triangles and the area of the rectangles and adding them together, we can find the areas of the trapezoids created by the gridlines on the x-axis. Let's also say we're looking at these trapezoids from the sides; they all have a height of 1.

The area of the first "trapezoid" (It's really a triangle, but I'm calling it a trapezoid for continuity's sake) is $1*\frac{0+1}{2}$ which is equal to $\frac{1}{2}$ .

The area of the second trapezoid is $1*\frac{1+3}{2}$ which is equal to $2$

The area of the third trapezoid is $1*\frac{3+6}{2}$ which is equal to $\frac{9}{2}$ .

Something to note about these numbers is that they are half of the square numbers (See the footnote for why this happens). So we need to find the sum of the squares from 1 to 2017 (We'll just take the last 3 digits of this since we would have to divide it by 2 and then multiply it by two again).

The sum of the squares from 1 to n is given by $\frac{(n)(n+1)(2n+1)}{6}\ = \frac{2017*2018*4035}{6}\ = 1009*2017*1345 = 2737280785$ , so the answer is 785 .

Footnote: The values we are adding together are $\binom{n}{2}$ and $\binom{n+1}{2}$ . The product of these is $\frac{n*(n-1)}{2}+\frac{(n+1)*n}{2}$ . When you simplify this fraction, you are left with just $n^2$ .