Reflections

Geometry Level 3

A unit circle $\Omega$ centered at $M$ has three points $A, B, C$ on its circumference such that $\angle AMB=\frac { 1 }{ 2 } \angle BMC$ . Point $P$ is the reflection of $M$ about $\overline{AB},$ point $Q$ is the reflection of $M$ about $\overline{BC},$ and point $S$ is the reflection of $Q$ about $\overline{BP}$ .

As $B$ varies on $\Omega$ $($ and so does $C$ satisfying the above condition $)$ with $A$ fixed, point $S$ traces a path $\gamma.$ Then, what is the largest possible distance that two points on $\gamma$ can be away from each other, i.e. what is $\max _{ X,Y\in \gamma } |XY| ?$

Notes:

Two angle measures that are an integer multiple of $360°$ apart are considered to be equal; for example, if $\angle AMB=190^\circ$ , then $\angle BMC=380^\circ\equiv 20^\circ$ .
When two points fall onto each other, reflection about their axis becomes point reflection.

Bonus:

What can be said about the angle $\angle SMA ?$

The answer is 4.

1 solution

Nick Kent
Jan 23, 2019

Since all symmetrical operations were conducted around lines containing point B, we get $BM = BP = BQ = BS = 1$ .

Let $\angle AMB=\alpha$ , then $\angle BMC=2\alpha$ . Triangles $\Delta ABM$ and $\Delta BCM$ are isosceles meaning $\angle CBM=\frac { \pi }{ 2 } -\alpha$ and $\angle ABM=\frac { \pi }{ 2 } -\frac { \alpha }{ 2 }$ .

Due to symmetry $\angle CBQ=\frac { \pi }{ 2 } -\alpha$ and $\angle ABP=\frac { \pi }{ 2 } -\frac { \alpha }{ 2 }$ . Thus $\angle QBP=2\pi -\angle CBQ-\angle CBM-\angle ABM-\angle ABP=3\alpha$ and $\angle PBS=3\alpha$ .

And finally, $\angle MBS=2\pi-\angle PBS-\angle QBP-\angle CBQ-\angle CBM = \pi-4\alpha$ . Triangle $\Delta MBS$ is also isosceles, $\angle BMS = 2\alpha$ .

That means, $\angle AMS=\alpha$ and $MS=2MBsin(2\alpha)=2MBsin(2\alpha)$ . Thus the path traced by point S is described by equation: $r = 2cos(2\phi)$ , where point M is the origin.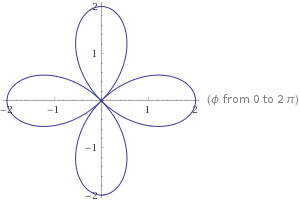 This equation describes a rose curve with four petals, maximum distance from point M amounts 2, meaning that maximum distance between two points on the curve reaches $2+2=\boxed{4}$ .

Reflections

The answer is 4.

1 solution

0 pending reports