Triangular Madness

Let $X$ be the point of intersection of the straight lnies $AE$ adnd $GD$ .
Let $Y$ be the point of intersection of the straight lnies $AE$ adnd $FC$ .

$AP = PD$ and $FC \| GD$ . By midpoint theorem, $AY=XY$ and $AY +XY = AX = 2XY$ .

$\begin{aligned} BD &=& \frac{BC}2 = DC \\ BE&=& ED = \frac{BC}4 \\ \therefore \frac{ED}{DC} &=& \frac12 \end{aligned}$

$GD \| FC$ , so by basic proportionality theorem,

$\begin{aligned} \frac{ED}{DC} &=& \frac{EX}{XY} \\ \frac12 &=& = \frac{EX}{XY} \\ \frac{EX}{2XY} &=& \frac14 \\ \frac{EX}{AX} &=& \frac14 \end{aligned}$

$\frac{A(\triangle XED)}{A(\triangle AXD)} = \frac14$

Applying componendo

$\frac{A(\triangle AED)}{A(\triangle (AXD) } =\frac54 \\ \frac{A(\triangle ABC)}{4 \cdot A(\triangle (AXD) } =\frac54 \\ \frac{A(\triangle ABC)}{ A(\triangle (AXD) } =5 \\ A(\triangle (AXD) = \frac{A(\triangle ABC)}5 = \frac{12345}5 =\boxed{2469} .$

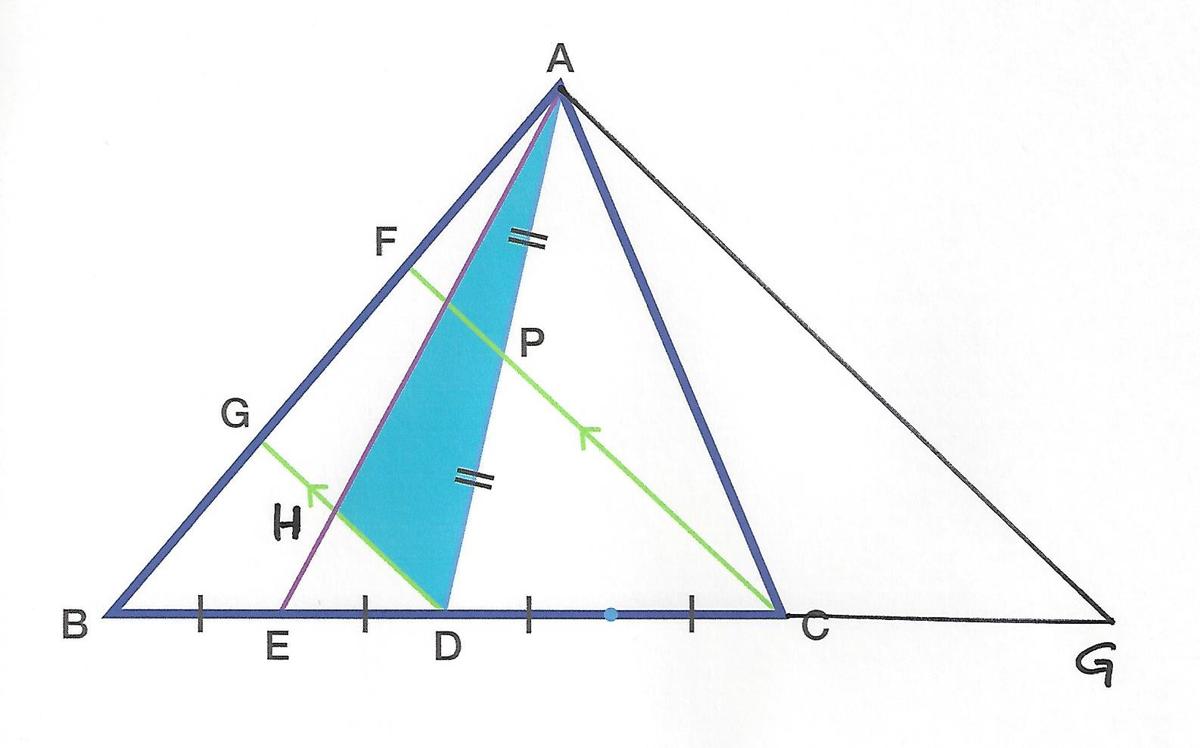
Extend line $EC$ to line $EG$ such that $DC = CG$ , and draw line $AG$ . Then triangle $EDH$ is similar to triangle $EGA$ , but in proportion of $ED:EG = 1:5$ . Hence, the altitude of triangle $EDH$ is $\dfrac{1}{5}$ of altitude of triangle $EGA$ . Given that the area of triangle $EDA$ is $\dfrac{1}{4}$ of triangle $BCA$ , and that the area of triangle $DAH$ is $1-\dfrac{1}{5}=\dfrac{4}{5}$ of triangle $EDA$ , the area of triangle $DAH$ is $\dfrac{1}{4}\cdot \dfrac{4}{5} = \dfrac{1}{5}$ of triangle $BGA$ , so that the area is $\dfrac{1}{5}\cdot 12345=2469$ .