Pure Pythagoras
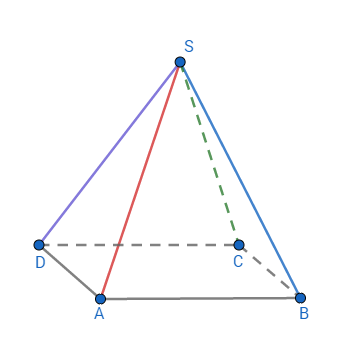
is a rectangular based pyramid, with being its apex. If and , what is the length of ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let E be the foot of the pyramid's height S E , a the length of the side A B and b the length of the side B C of the pyramid's rectangular basis. Drop four lines from E so that each of them is perpendicular to the lines that contain each of A B C D 's sides, and let p be the length of the line perpendicular to line A B and q the length of the line perpendicular to line B C . In case E is inside A B C D , by Pythagoras' Theorem, we have:
A E 2 = p 2 + q 2
B E 2 = ( a − p ) 2 + q 2
C E 2 = ( a − p ) 2 + ( b − q ) 2
D E 2 = p 2 + ( b − q ) 2
Sum up first and third equation, and then second and fourth to get:
A E 2 + C E 2 = B E 2 + D E 2
In case E is outside A B C D , in equations above we would use a + p or b + q depending on where the point E is, but that doesn't affect the result.
Again, by Pythagoras' Theorem:
S A 2 = A E 2 + S E 2
S B 2 = B E 2 + S E 2
S C 2 = C E 2 + S E 2
S D 2 = D E 2 + S E 2
Now:
S A 2 + S C 2 = A E 2 + C E 2 + 2 S E 2 = B E 2 + D E 2 + 2 S E 2 = S B 2 + S D 2
So:
S A 2 + S C 2 = S B 2 + S D 2
From this we can easily calculate the length of S D :
S D = S A 2 − S B 2 + S C 2 = 5 − 8 + 4 = 1 = 1