A geometry problem by Ossama Ismail
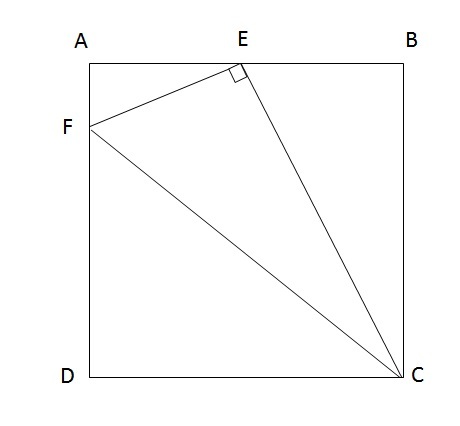 In the square
,
is the midpoint of
. A line is drawn from
, perpendicular to
, and intersecting
at
.
In the square
,
is the midpoint of
. A line is drawn from
, perpendicular to
, and intersecting
at
.
Find the ratio of to .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Without loss of generality, let the length of the side of the square be 2. Since E is the midpoint of AB, this means that AE = EB = 1. By the Pythagorean Theorem applied to triangle CEB, we find EC = Sqrt(5). Similarly, applying the Pythagorean Theorem to triangles AFE, FDC, and FEC, we find that AF = 1/2, FD = 3/2, and FE = (1/2) Sqrt(5). We then note that tan(angle BCE) = 1/2 and tan(angle ECF) = (1/2) sqrt(5) / sqrt(5) = 1/2. Therefore, angle BCE = angle ECF, so that angle BCF is twice the measure of angle BCE (i.e., the ratio is 2:1).