Inside And Outside
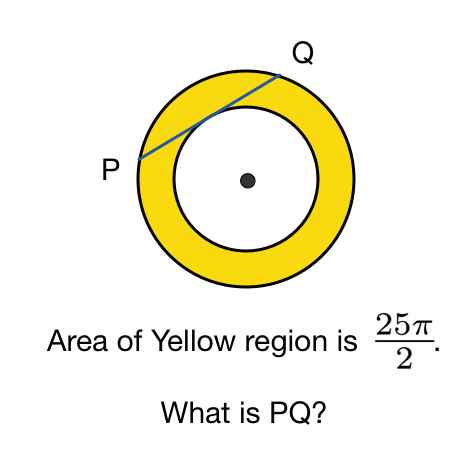
The above shows an annulus , a region bounded by two circles sharing the same center. straight line P Q is a tangent to the circumference of the small circle and is a chord of the big circle.
If the area of annulus is 2 2 5 π , find the length P Q .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A clear solution, nice!
Area of annulus = π r l 2 − π r s 2 = π ( r l 2 − r s 2 ) = 2 2 5 π . So r l 2 − r s 2 = 2 2 5 .
We draw a right triangle with vertices at the centre of the circle(s), the tangent point, and Q. Let's call the angle at the centre of the circle θ .
Immediately we can see that the length of the adjacent side to that angle is the radius of the smaller circle, r s . So we can say that r l cos θ = r s (because the hypotenuse of our right triangle is the radius of the large circle, r l ). We substitute this expression for r s back into our first equation:
r l 2 − ( r l cos θ ) 2 = r l 2 ( 1 − cos 2 θ ) = 2 2 5 ⟹ r l 2 sin 2 θ = 2 2 5 (trigonometric identity).
So r l sin θ = 2 5 , and we recognize this as being the opposite side to θ ! We also notice that this value represents only half of the length of PQ. So the answer is 2 × 2 5 = 5 2 .
Nicely explained. I upvoted your solution (+1) :)
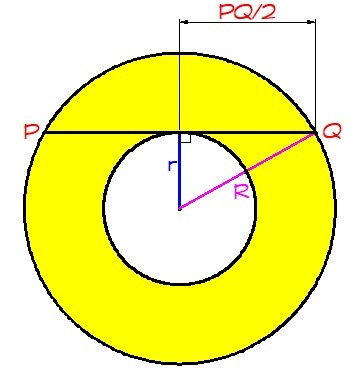
From the figure, the area of the annulus is equal to ( 2 P Q ) 2 π , so
( 2 P Q ) 2 π = 2 2 5 π
P Q = 5 0 = 5 ( 2 ) answer
 A
y
e
l
l
o
w
=
π
(
R
2
−
r
2
)
A
y
e
l
l
o
w
=
π
(
R
2
−
r
2
)
2 2 5 π = π ( R 2 − r 2 )
2 2 5 = R 2 − r 2
By pythagorean theorem,
( 2 P Q ) 2 = R 2 − r 2
4 P Q 2 = 2 2 5
P Q 2 = 5 0
P Q = 5 0 = 2 5 ( 2 ) = 5 2 ( 2 ) = 5 2
Relevant wiki: Circles Problem Solving - Basic
Let the radius of bigger circle and smaller circle is a and b .
So, shaded area= π a 2 − π b 2 = 2 2 5 π ⇒ a 2 − b 2 = 2 2 5
Let the contact point of tangent to smaller circle be F .
In △ F O Q .
O Q 2 = O F 2 + F Q 2
a 2 = b 2 + F Q 2
a 2 − b 2 = F Q 2
2 2 5 = F Q 2
F Q = 2 5 2
And we know that 2 F Q = P Q .
∴ P Q = 2 × 2 5 2 = 5 2