A geometry problem by Paola Ramírez
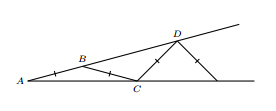
A figure is built by isosceles triangles as the image shows. , then and so on. If , how many isosceles triangles can you draw?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Now let’s find ∠ C B D (Triangle 2)
∠ C B D = 2 ∠ C A B ∠ C B D = 2 ( 1 7 ∘ ) ∠ C B D = 3 4 ∘
Now find ∠ E D F (Triangle 3)
∠ E D F = 2 ∠ C B D ∠ E D F = 2 ( 3 4 ∘ ) ∠ E D F = 6 8 ∘
Between △ B C D and △ E D F , there must be another triangle ( △ C D E (Triangle 4))
There is no way Triangle 6 existed because one of the base angle of the triangle = 6 8 ∘ × 2 = 1 3 6 ∘
We cant draw such a triangle because then the third vertex would not be formed because the equal sides would never intersect as they move apart
Since Triangle 6, 7, 8, 9, ... is no longer existed, let’s find out about Triangle 5
∠ D E C = 2 1 8 0 ∘ − ( 1 8 0 ∘ − 6 8 ∘ − 3 4 ∘ ) = 5 1 ∘ ∠ D E F = 1 8 0 ∘ − 2 ( 6 8 ∘ ) = 4 4 ∘ ∠ F E G = 1 8 0 ∘ − 5 1 ∘ − 4 4 ∘ = 8 5 ∘ ∠ F G E = 8 5 ∘ ∠ E F G = 1 8 0 ∘ − 2 ( 8 5 ∘ ) = 1 0 ∘ ( △ E F G (Triangle 5))
So there is 5 isosceles triangle that can fit in
It’s the only solution i can think of :)