Rotating Triangles
Let △ A B C and △ C D E be equilateral triangles of the same size, and ∠ B C D = 8 0 ∘ between them. Find the measure of ∠ B A D in degrees.
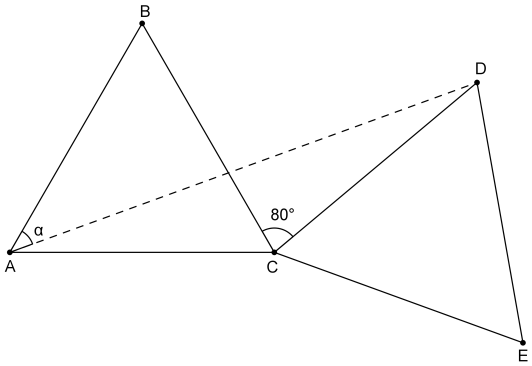
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How is AC=CD or how is the triangle isosceles because it is not given that they are equal or congruent equilateral triangle?
Log in to reply
It needs to be specified in the problem statement that the triangle are the same size.
Log in to reply
Thanks. I have edited the problem accordingly.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator who can fix the issues.
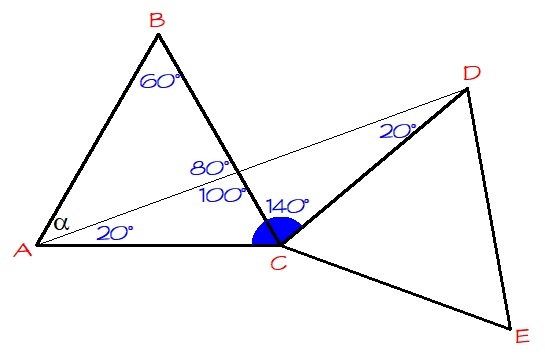 α
=
1
8
0
−
6
0
−
8
0
=
4
0
α
=
1
8
0
−
6
0
−
8
0
=
4
0
This is a very long solution. You computed many angles.
Consider isosceles △ A C D .
∠ A C D = 6 0 + 8 0 = 1 4 0 ∘
Since A C = C D , ∠ A D C = ∠ D A C = 2 1 8 0 − 1 4 0 = 2 0 ∘ . It follows that ∠ α = 4 0 ∘ .
Relevant wiki: Properties of Isosceles Triangles
∠ A C D = 1 4 0 ° and △ A C D is isosceles ⇒ ∠ D A C = ∠ C D A = 2 0 °
∠ B A D = 6 0 ° − 2 0 ° = 4 0 °