A strange quadrilateral
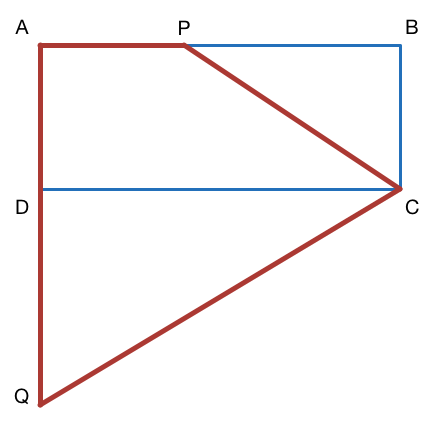 Consider a rectangle which has a diagonal of length 6. If
P
is a point on side
A
B
such that
∣
A
P
∣
=
∣
A
D
∣
,
and
Q
is a point on the extension of side
A
D
such that
∣
A
Q
∣
=
∣
A
B
∣
,
what is the area of the quadrilateral
A
P
C
Q
?
Consider a rectangle which has a diagonal of length 6. If
P
is a point on side
A
B
such that
∣
A
P
∣
=
∣
A
D
∣
,
and
Q
is a point on the extension of side
A
D
such that
∣
A
Q
∣
=
∣
A
B
∣
,
what is the area of the quadrilateral
A
P
C
Q
?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
Please upvote It if you like it

First of all seeing the conditions in the questions I assumed that A B C D is a square and Q coincides D and P coincides B
Now as B P is a diagonal ∴ B P = 2 ⋅ A B
i.e 6 = 2 ⋅ A B ⇒ A B = 3 2
As area of square is A B 2 where A B is side of a square
⇒ ∴ Area= ( 2 3 ) 2 ⇒ 1 8 c m 2
Hence the answer is ⇒ 1 8
Having found the answer under such a specific assumption, you should then proceed to try and solve the general case.
See my response above.
Very imaginative. The solution is not a trial and error approach. As P and the rectangle are arbitrary, they can be moved provided the conditions are not changed.
The only problem is the use of the word assume. Yes, a square is rectangle but a rectangle as we know is not necessarily a square.
But I understand why and how he came up with the assumption, the solution is very creative nonetheless. I guess it would be easier to understand to see what happens if point D is moved closer to Q. To be consistent with the conditions, P must move closer to B.
Because BD=6 Then, A D 2 + A B 2 = 6 2 = 36
From above figure total area is= A D 2 + 2 1 PX CX + 2 1 DQ CD
→ A D 2 + 2 1 AD (AB-AD) + 2 1 (AB-AD) AB
→ A D 2 + 2 1 (AB AD - A D 2 + A B 2 - AB AD)
→ A D 2 + 2 1 ( A B 2 - A D 2 )
→ 2 1 (2 A D 2 + A B 2 - A D 2 )
→ 2 1 A D 2 + A B 2
→ 2 3 6
→ 18
So, Total area is 18.
Lets create straight line AC and straight line PQ.
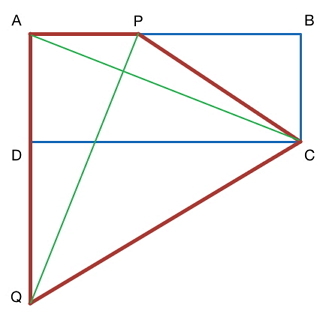
AC is perpendicular to PQ. A r e a A P C Q = 2 A C × P Q = 2 6 × 6 = 1 8 u n i t 2
Area of A P Q C = △ A C Q + △ A P C .
As A P = A D = B C △ A P C area is 2 1 ( A D ) ( A D ) = 2 1 A D 2 .
As A B = D C = A Q △ A Q C area is 2 1 ( A B ) ( A B ) = 2 1 A B 2 .
Thus A P Q C area is ( 2 1 ) ( A B 2 + A D 2 )
We know that A B 2 + A D 2 = 6 2 = 3 6
So area A P Q C = ( 2 1 ) ( A B 2 + A D 2 ) = ( 2 1 ) ( 3 6 ) = 1 8
i did it the same way as you did
According to I l y a A n d r e e v , 2 x 2 + 2 x y + y 2 = 3 6 .
The assumption of one M e h u l C h a t u r v e d i can be explained by similarity.
A P = A D and A B = A Q . All are sides of two squares. All squares are similar.
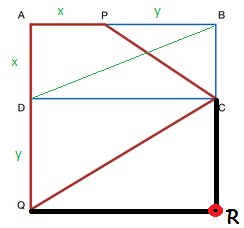
Refer to the figure above. A B R Q is a square. Its area is A A B R Q = ( x + y ) 2
L A T E X
The area of A P C Q can be solve by subtracting the areas of Δ P B C and Δ C R Q .
A Δ P B C = 2 1 x y
A Δ C R Q = 2 1 y ( x + y )
L A T E X
A A P C Q = A A B R Q − A P B C − A C R Q
A A P C Q = ( x + y ) 2 − 2 1 x y − 2 1 y ( x + y )
A A P C Q = x 2 + 2 x y + y 2 − 2 1 x y − 2 1 x y − 2 1 y 2
A A P C Q = x 2 + x y + 2 1 y 2
L A T E X
Solve for y 2 in 2 x 2 + 2 x y + y 2 = 3 6
y 2 = 3 6 − 2 x 2 − 2 x y ← Plug this to the other equation.
A A P C Q = x 2 + x y + 2 1 ( 3 6 − 2 x 2 − 2 x y )
A A P C Q = x 2 + x y + 1 8 − x 2 − x y
A A P C Q = 1 8
L A T E X
L A T E X
PS. Help me know how to tag! lol Please upvote. :)
Let's do some name calling: A P = x , P B = y . Using the information given to us, we can also write A D = x ; A B = x + y ; D Q = A Q − A D = ( x + y ) − x = y .
Now let's write the expression for the diagonal BD, applying the Pythagorean theorem to, say, Δ A D B : B D 2 = A B 2 + A D 2 B D 2 = ( x + y ) 2 + x 2 = 2 x 2 + 2 x y + y 2 = 3 6
We might need it somewhere, who knows? Anyway, thinking about the area of the polygon we want to find, the first urge is to break it into two parts: trapezoid A P C D and right triangle D Q C . Their corresponding areas are A A P C D = 2 x + ( x + y ) x = ( x + 2 y ) x = x 2 + 2 x y and A Δ D Q C = 2 1 y ( x + y ) = 2 1 y 2 + 2 x y
Let's sum them up: A A P C Q = x 2 + 2 x y + 2 x y + 2 y 2 = 2 1 ( 2 x 2 + 2 x y + y 2 )
Look at you! You're just half of B D 2 , or simply 2 3 6 = 1 8