This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since there are already sources to derive the maximized areas of the polygon, I suggest those done with the problem to go even further with geometry challenges. Good luck!
Bonus 1: Generalize this for the sector of arbitrary angle 0 ∘ < α ≤ 3 6 0 ∘ and bounded polygon of n edges.
Caution: You need to understand how the sector is formed before you attempt to perform any calculation since a polygon may not be bounded for all α .
Bonus 2: What if suppose from Bonus 1 , we determine the minimum area of the polygon bounding the circle?
Bonus 3: What if suppose we determine the maximum area under the general ellipse? What about the minimum area?
Log in to reply
Bonus 2: The minimum area is 0, since we can chose the area to be arbitrary small by placing the vertices of the polygon as close as possible to one of the vertex at the diameter.
Bonus 3: This is very similar to the problem with a circle. Since an ellipse can be seen as a uniformly stretched circle, we can similarly stretch the polygon achieved with a circle to match that of the ellipse.
Log in to reply
Fine. Let's suppose we have the segment bounded by the circle. I adjusted the details for Bonus 2 and Bonus 3 , so that the polygon bounding the circle is not zero. Sorry for the complication. :)
Here is what I mean by circumscribed polygon:

Bonus 1 is really interesting. For example, with 1 8 0 ∘ < α < 3 6 0 ∘ , the best quadrilateral is still this trapezium that we found!
This arises due to the non-convexity, which makes the diameter a much more attractive side to use.
I wonder for what value (if any) of the number of sides, this no longer holds.
NEW I revised Bonus 2 and Bonus 3 since I made the typo for that one.
@Paul Hindess @Michael Huang Very nice reflection trick!
Thanks, Michael. The solution I was expecting - and beautifully presented! (-:
Log in to reply
I belive the condition of "One of the sides of the quadrilateral has to lie on the diameter." can be removed, by making that the first fact to be proven.
It is obvious when we use a Jensen's convexity argument. Do you see a non calculus / lots of algebra approach?
Log in to reply
I've removed the "One of the sides..." bit. Only put it in there in imitation of the Inspirations, but never quite understood why it was there... Surely it wasn't necessary in the forerunners either?
David's approach below was how I imagine I'd have approached it algebraically...
With no prior intuitive grasp of the problem, I did mine as a maximisation using this setup:
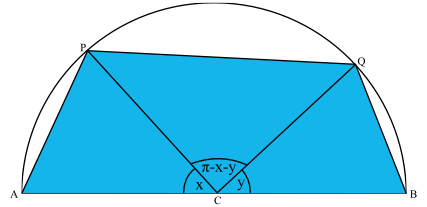
∣ A C ∣ = ∣ C B ∣ , so △ A P C , △ P Q C and △ C Q B are isosceles, since C is the centre of A B
Using the sine form for the area of a triangle ( A = 2 1 a b sin C ), we come up with the function for the area of the quadrilateral:
f ( x , y ) = z = 2 1 ( 1 ) ( 1 ) sin x + 2 1 ( 1 ) ( 1 ) sin y + 2 1 ( 1 ) ( 1 ) sin ( π − x − y )
z = 2 1 ( sin x + sin y + sin ( π − x − y )
Observing that sin ( π − A ) ≡ s i n ( A )
z = 2 1 ( sin x + sin y + sin ( x + y ) )
Taking partial derivatives and equating to zero for maximisation
δ x δ z = cos x + cos ( x + y ) = 0 ( 1 )
δ y δ z = cos y + cos ( x + y ) = 0 ( 2 )
Subtracting equation (2) from equation (1)
cos x − cos y = 0
For x , y ∈ ( 0 , π ) , we conclude that x = y , since f ( x ) = cos x is one-to-one in the interval
Now the maximisation problem is simplified. We can now write our area function in the form z = g ( x )
z = 2 1 ( 2 sin x + sin 2 x )
Taking the derivative and maximising by equating to zero
d x d z = cos x + cos 2 x = 0
Observing the double-angle identity cos 2 x ≡ 2 cos 2 x − 1
cos x + 2 cos 2 x − 1 = 0
( 2 cos x − 1 ) ( cos x + 1 ) = 0
cos x = 2 1 , − 1 ⇒ x = 3 π , π
Since π is not in the domain for x , we conclude that x = 3 π
Substituting back into our area function, we find that
z = 2 1 ( 2 sin 3 π + sin 3 2 π ) = 2 1 ( 2 ( 2 3 ) + 2 3 ) = 4 3 3 = 1 . 2 9 9 . . .
Good approach. Do you know how to apply jensen's inequality to this problem? That would save a lot of the work on derivatives.
Calvin Sir u r great!!!
This was my sister's high school graduation project years ago, which is researching the different shapes of rain gutters.
Note: Another way to visualize this is to draw the chords of the same length. The alternative mathematical proof is here .
So by slicing the circle in half as shown in the diagram, we obtain the semicircle, now containing inscribed polygon of 4 edges (because the slice creates an extra edge). Here is the new diagram: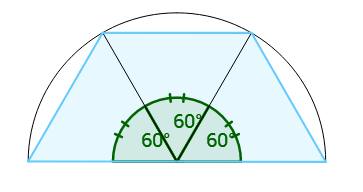 Figure 2. Sliced circle, now the semicircle
Thus, since there are three equivalent isosceles triangles of
6
0
∘
angle and two edges of length
1
, by the following formula,
A
=
2
1
b
c
sin
(
α
)
we have
maximized area of the inscribed polygon
=
3
⋅
area of one isosceles triangle
=
2
3
sin
(
6
0
∘
)
=
4
3
3
≈
1
.
2
9
9
0
3
8
Figure 2. Sliced circle, now the semicircle
Thus, since there are three equivalent isosceles triangles of
6
0
∘
angle and two edges of length
1
, by the following formula,
A
=
2
1
b
c
sin
(
α
)
we have
maximized area of the inscribed polygon
=
3
⋅
area of one isosceles triangle
=
2
3
sin
(
6
0
∘
)
=
4
3
3
≈
1
.
2
9
9
0
3
8
In case you want to take the challenges even further, see comment under my solution!