Mind the Interval!
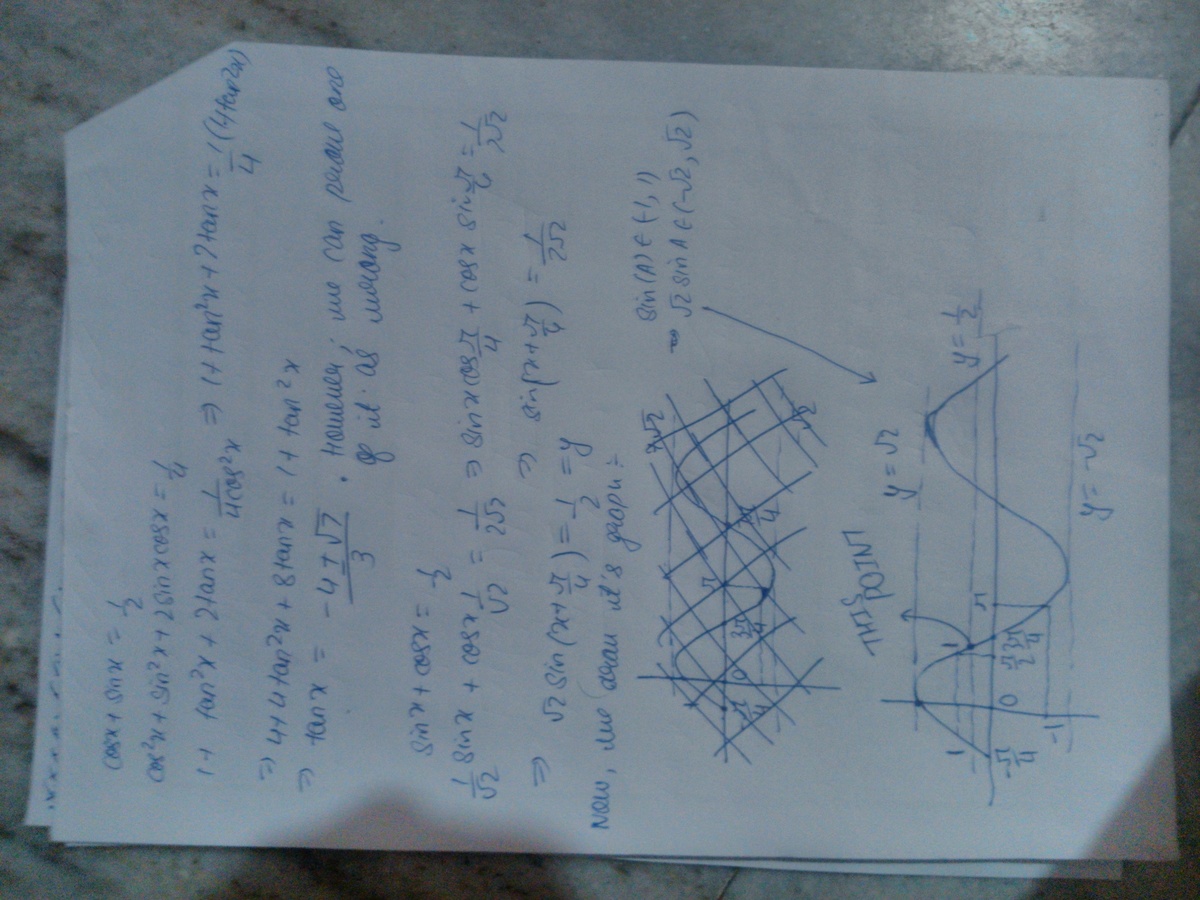
If cos x + sin x = 2 1 , find the value of tan x , where x ∈ ( 0 , π ) .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Jason, I tried getting "report", but it did not work. Anyway, I think the solution is wrong. The roots are (-4 - sqrt(7))/3 = -2.7152 and (-4 + sqrt(7)/3, and tan(114.2955) = - 2.7152 and tan(155.7045) = -.4514, both between 0 and 180, so I think both A and D are correct. my apologies if wrong. Ed Gray
I wasnt sure as to how to draw a graph on the comp., so i had to go with images.

Nice solution. Up voted.
Log in to reply
Thanks. Check out my problem "Motion and Some Calculus" on my profile. :D
By squaring sin x + cos x = 2 1 one has sin x cos x = − 8 3 .
So, sin x and cos x are the roots of 8 y 2 − 4 y − 3 = 0 .
As 0 < x < π , we have sin x = 4 1 + 7 and cos x = 4 1 − 7 .
Finally, tan x = − 3 4 + 7 .
since \sinx+\cosx=\sqrt{2}sin[x+\frac{\pi}{4}]=\frac{1]{2}, we can think of the triangle below. {: .center} \(AE=2\sqrt{2}, AB=1, BE=sqrt{7} and thus tan θ = f r a c 1 s q r t 7 .
We have to find \tanx=-\tan(\theta+\frac{\pi}{4}=\frac(1+\tan\theta}{1-\tan\theta|=-\frac{4+\sqrt{7}}{3}
Firstly, we square both the sides to get 1 + sin 2 x = 4 1
⟹ sin 2 x = 4 − 3
Now, we use the identity sin 2 x = 1 + tan 2 x 2 t a n x to get a quadratic equation
3 tan 2 x + 8 t a n x + 3 = 0
⟹ t a n x = 3 − 4 ± 7
Now, we prove that only one of these solutions works.
First of all, to get a better picture, we take approximations.
7 ≈ 2 . 7 and thus 3 − 4 + 7 ≈ 3 − 1 . 3 and similarly
3 − 4 − 7 ≈ 3 − 6 . 7
Now, we know that t a n x < 0 ⟹ 2 π < x < π (since x ∈ [ 0 , π ] ) ⟹ s i n x > 0 and c o s x < 0
But s i n x + c o s x = 2 1 > 0 .
Thus,
s i n x > ∣ c o s x ∣
This means that the numerator has to be greater than the denominator in ∣ t a n x ∣ and thus
t a n x = 3 − ( 4 + 7 )