A geometry problem by Rahil Sehgal
Geometry
Level
3
In a triangle 𝐴𝐵𝐶, let 𝐼 denote the incenter. Let the lines 𝐴𝐼, 𝐵𝐼 and 𝐶𝐼 intersect the incircle at 𝑃, 𝑄 and 𝑅, respectively. If ∠𝐵𝐴𝐶 = 40, what is the value of ∠𝑄𝑃𝑅 in degrees?
50
40
55
60
45
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
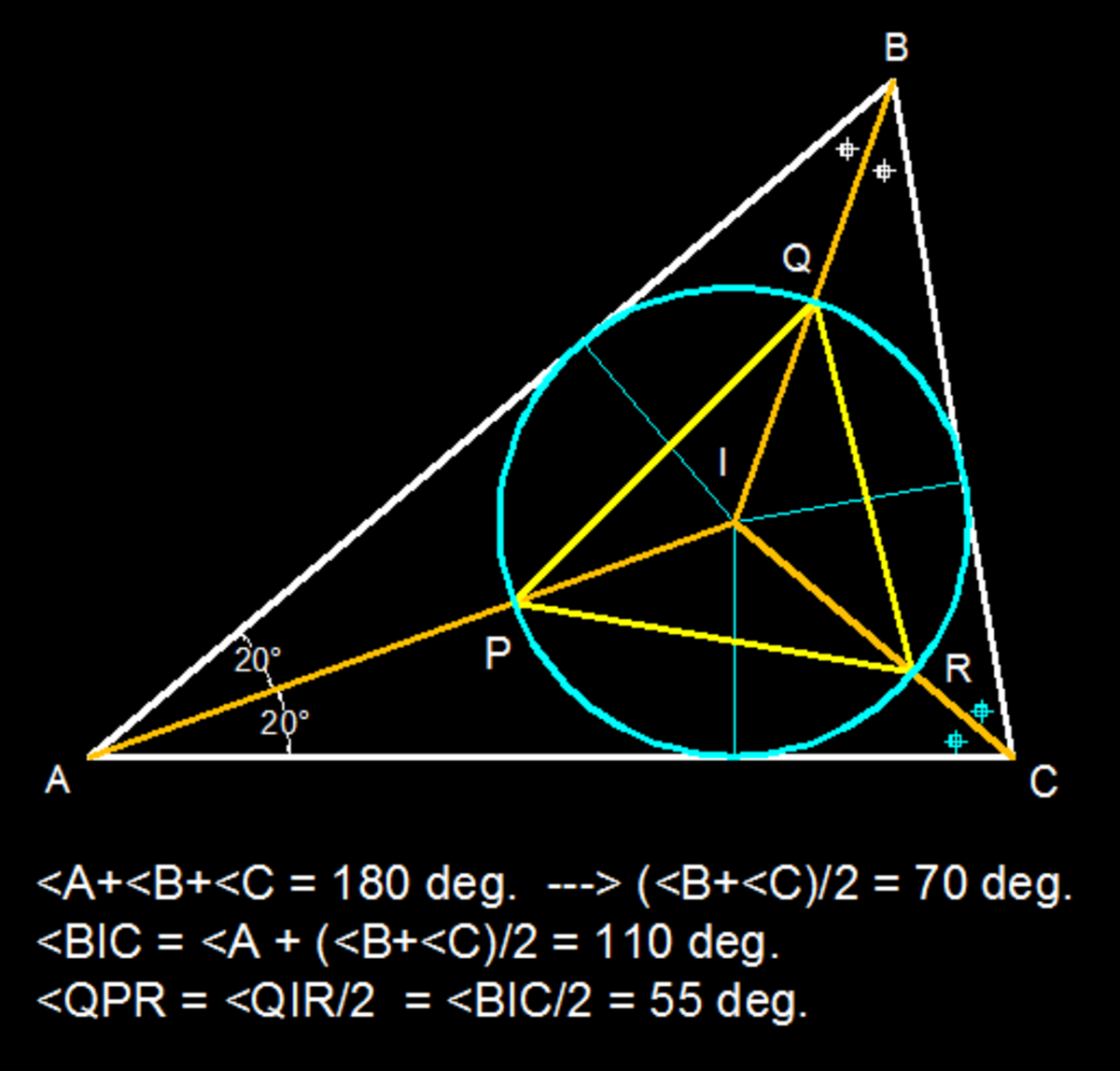
In the red quadrilateral A B O C angle B A C = 4 0 ∘ and ∠ A B O + ∠ O C A = 2 1 ( ∠ A B C + ∠ B C A ) = 7 0 ∘ .
That leaves ∠ B O C = 3 6 0 ∘ − 4 0 ∘ − 7 0 ∘ = 2 5 0 ∘
∠ Q O R = external angle B O C = 3 6 0 ∘ − 2 5 0 ∘ = 1 1 0 ∘
∠ Q P R = 2 1 ∠ Q O R = 2 1 1 0 = 5 5 ∘