A geometry problem by Ranganath Govardhanam
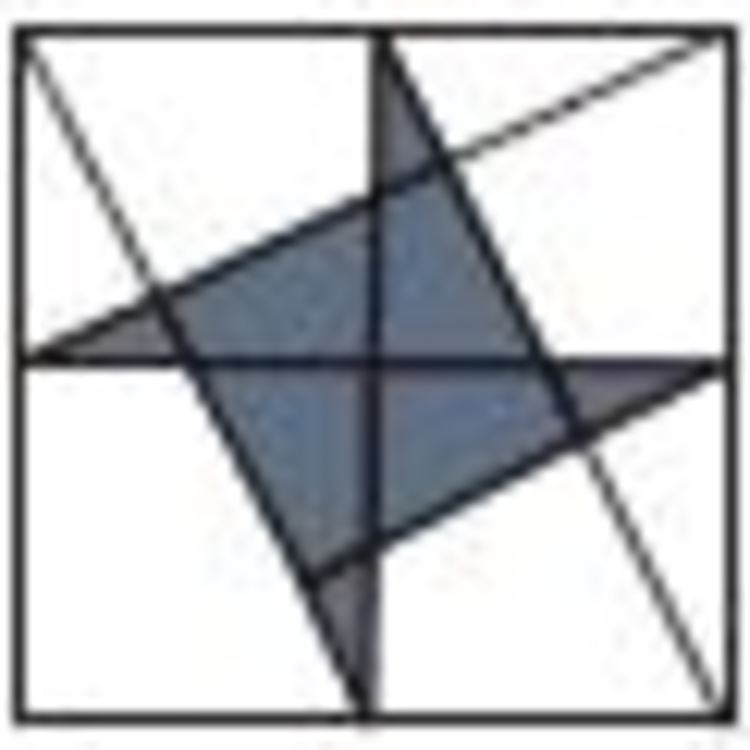 In the diagram given, each corner of the shaded star is at the midpoint of the sides of the larger square. What fraction of the area of the larger square is covered by the star?
In the diagram given, each corner of the shaded star is at the midpoint of the sides of the larger square. What fraction of the area of the larger square is covered by the star?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 The area required is 4 times the green area
C
D
E
.
D
i
s
m
i
d
p
o
i
n
t
o
f
C
B
.
D
E
∥
B
A
.
∴
C
D
E
=
4
1
A
B
C
.
A
B
C
=
4
1
B
i
g
S
q
u
a
r
e
.
∴
4
∗
C
D
E
=
4
∗
4
1
A
B
C
=
4
1
B
i
g
S
q
u
a
r
e
.
4
1
The area required is 4 times the green area
C
D
E
.
D
i
s
m
i
d
p
o
i
n
t
o
f
C
B
.
D
E
∥
B
A
.
∴
C
D
E
=
4
1
A
B
C
.
A
B
C
=
4
1
B
i
g
S
q
u
a
r
e
.
∴
4
∗
C
D
E
=
4
∗
4
1
A
B
C
=
4
1
B
i
g
S
q
u
a
r
e
.
4
1
The shaded square has edge with side length: 5 1 Each of three-angles beside of this shaded star is a right three-angles with one side of right angle is equal to: 2 × 5 1 The other side with length: 4 × 5 1 So it is easy to get area of the shaded star is: 5 1 × ( 1 + 4 1 ) = 4 1