A geometry problem by Riel Diala
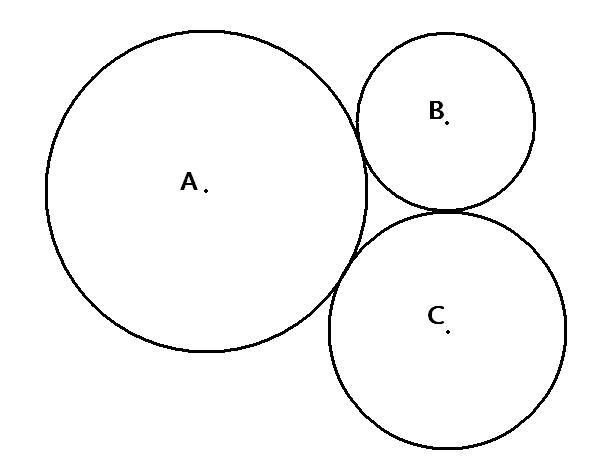 The length of line segment AB is 24 units.
The length of line segment AB is 24 units.
The length of line segment AC is 25 units.
The length of line segment BC is 19 units.
QUESTION: What is the radius of circle A?
NOTE: Figure may or may NOT be drawn to scale, since this math problem can be solved without a picture.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
- A R + B R = 2 4
- A R + C R = 2 5
- B R + C R = 1 9
( A R + B R ) + ( A R + C R ) − ( B R + C R ) 2 A R A R = 2 4 + 2 5 − 1 9 = 3 0 = 1 5
Let the radius of circle A be a
Let the radius of circle B be b
Let the radius of circle C be c
eq1: a + b = 24
eq2: b + c = 19
eq3: a + c = 25
There are many ways in doing the "systems of equations" but here's one way:
From eq1, we find a formula for b in terms of a
b = 24 - a
Since we have an equation for b, we substitute it for b in eq2
(24-a) + c = 19
24 - a + c = 19
c - a = -5
and now we can find for c in terms of a
c = a - 5
Now we substitute the equation to c in eq3
a + (a - 5) = 25
a + a -5 = 25
2a - 5 = 25
2a = 30
a = 15
Therefore, the radius of circle A is 15 units.
Let the radius of
Circle A be a ,
Circle B be b ,
and, that of Circle C be c .
Now,
a + b = 2 4 → E q . 1
a + c = 2 5 → E q . 2
b + c = 1 9 → E q . 3
Adding E q . 1 and E q . 2 , we get,
2 a + b + c = 2 4 + 2 5
⇒ 2 a + ( b + c ) = 4 9
⇒ 2 a + 1 9 = 4 9 [From E q . 3 ]
⇒ 2 a = 3 0
⇒ a = 1 5
So, Radius of Circle A is a = 1 5