Awesome Geometry!

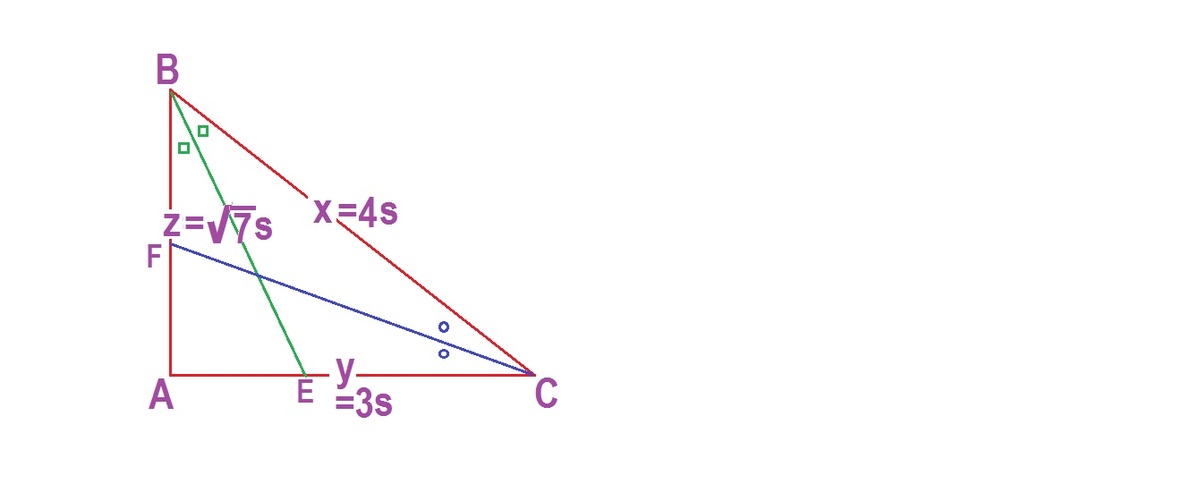
$\text{Let AB=z, BC=x, CA=y, Radius of circumcircle=R. S=2R in the sketch.}\\ So\ x=2R,\ y=\frac 3 2*R \implies\ \frac 4 3 *y=2R.\\ Using\ extended\ Sin\ Law,\ \ 2R=\dfrac x {SinA} =\dfrac y{SinB}.\\ Equating\ the\ two\ values\ of\ x,\ and\ y \ we\ get:-\\ SinA=1, \ so\ A=90, \ \ \ \ SinB=\frac 3 4,\ \ \implies\ SinC=\frac {\sqrt7} 4.\ \ \ \ \ \ \ \ \ \because\ \sqrt{4^2-3^2}=\sqrt7\\ So\ ABC\ is\ a\ right\ \Delta\ \sqrt7\!-\!3\!-\!4. CosB=\dfrac{\sqrt7}4,\ \ CosC=\sqrt 3 4.\\ But\ Cos\frac 1 2 \theta=\sqrt{\dfrac{1+Cos\theta} 2}.\\ \therefore\ Cos\frac12B=\sqrt{\dfrac{1+CosB} 2}=\sqrt{\dfrac{1+\frac{\sqrt7}4} 2},\ \ \ \ \ \ \ \ Cos\frac12C=\sqrt{\dfrac{1+CosC} 2}=\sqrt{\dfrac{1+\frac 34} 2}\\ \therefore\ BE=\dfrac{\sqrt7}{ Cos\frac12B}= \dfrac{\sqrt7}{ \sqrt{\dfrac{1+\frac{\sqrt7}4} 2} }= \dfrac{\sqrt7}{ \sqrt{\dfrac{4+\sqrt7} 8} }\ \ \ \ \ \ \ \ CF= \dfrac 3 { Cos\frac12C}=\dfrac 3{ \sqrt{\dfrac{1+\frac 3 4} 2} }= \dfrac 3 { \sqrt{\dfrac{4+3 } 8} } \\$ $\therefore\ \dfrac {BE}{CF}=\dfrac{\ \dfrac {\sqrt7} { \sqrt{\dfrac{4+\sqrt7} 8} } \ }{ \dfrac 3{ \sqrt{\dfrac 7 8} }}= \dfrac{ \dfrac 7 { \sqrt{4+\sqrt7} } }3=\dfrac{ \dfrac {7*\sqrt{4-\sqrt7}} { \sqrt{4+\sqrt7}*\sqrt{4-\sqrt7} } }3=\frac 7 9* \sqrt{4-\sqrt7}\\ =\frac 7 9* \sqrt{( \sqrt {\frac 7 2} - \sqrt{\frac 1 2} )^2 }=\dfrac{7\sqrt{14} - 7\sqrt2}{18}=\dfrac {a\sqrt b - a\sqrt c}{d}\\ (a+b) - (c+d)=(7+14) -(2+18) =\ \ \ \ \color{#D61F06}{1}$