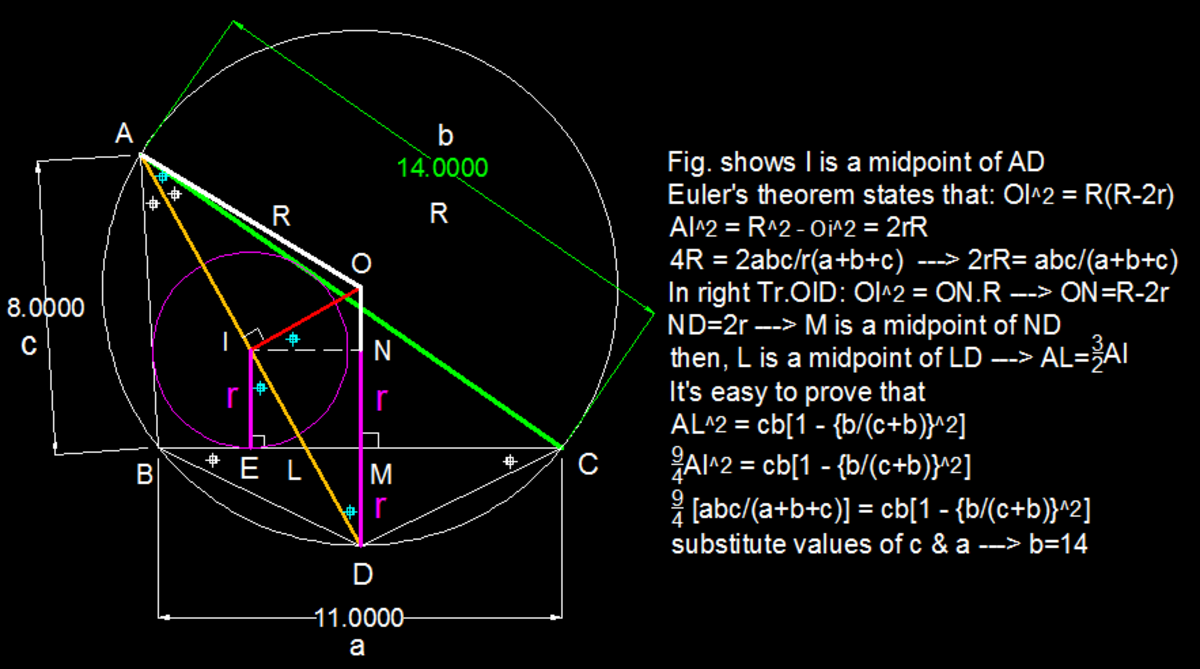
Relating the circle centers with the sides

Produce $AI$ to $P$ such that $PI = AI.$ Now, we obtain that $OI$ is the $\perp$ bisector of segment $AP$ Thus, $OP = AO$ $\Rightarrow$ The point $P$ lies on $\odot ABC$ . Join $PB , PC$ . Let $E$ and $F$ denote the midpoints of $AC$ and $AB$ respectively. Join $IF , OF , IE , OE$ . Let $AP$ intersect $BC$ at $Q$ . Trivial angle chasing in $\Delta AIO$ gives that $\angle OAI = \angle B/2 - \angle C/2$ and $\angle AOI = \angle A/2+ \angle C/2$ $\Longrightarrow$ In cyclic quad. $AOIF$ $\angle AIF = \angle AOC = \angle C.$ And, in cyclic quadrilateral $AIOE$ , $\angle AOE = \angle AIE = \angle B.$ Now, by the excenter lemma, $PB = PC = PI = AI$ Clearly, through ASA congruency rule, $\Delta PCQ \cong \Delta IAE$ and $\Delta PCQ \cong \Delta IAF$ $\Rightarrow$ $BQ = AF$ , similarly $QC = AE.$ Adding, $BQ + QC = AE + AF => a = \dfrac{b}{2}+ \dfrac{c}{2} => 2a = b + c => b = 2a - c = 2 * 11 - 8 = 22 - 8 = 14$