Drawing a unique triangle

I have a 15 move solution.

Let $H$ and $O$ be the orthocentre and circumcentre respectively, and the line as $l$ .

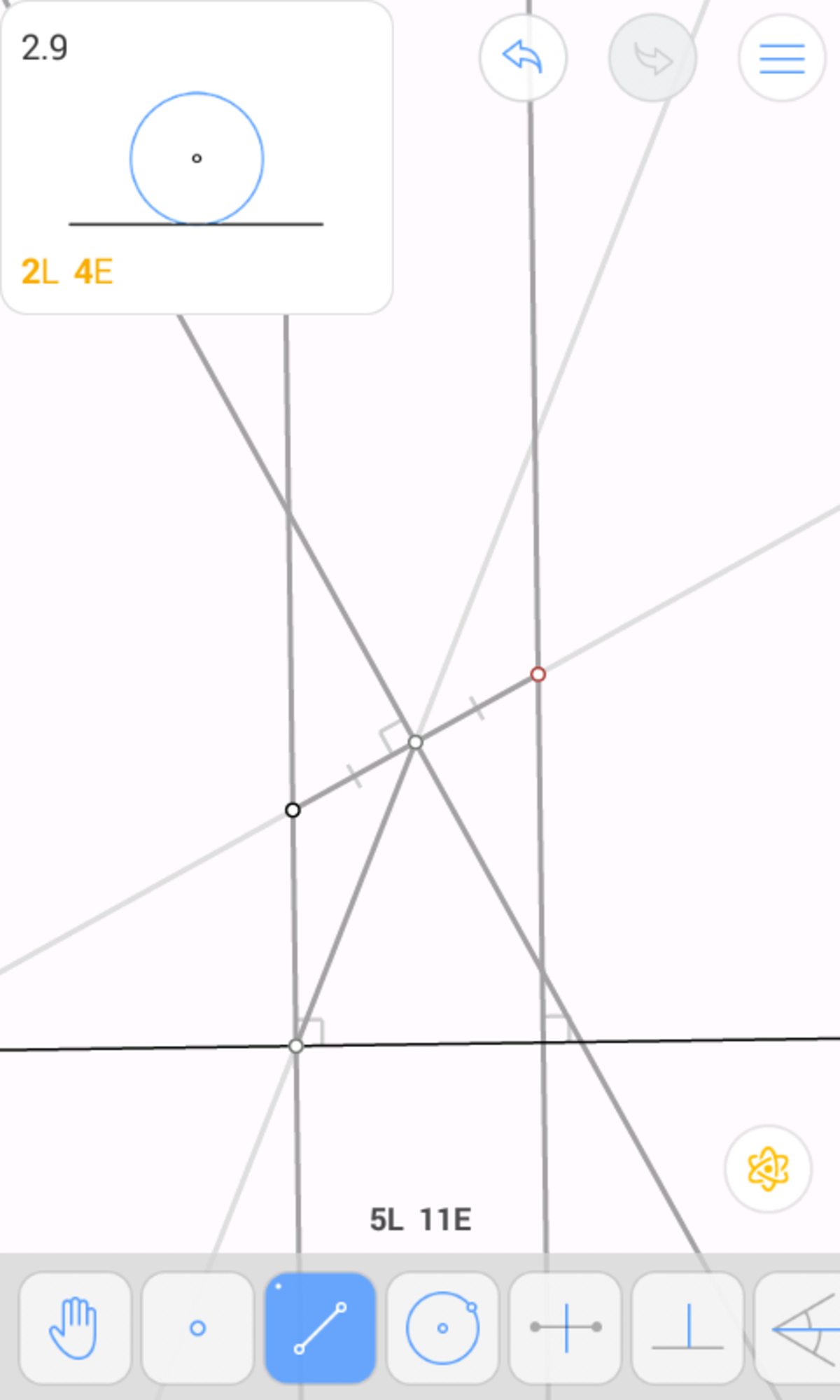
First, we will draw perpendiculars from $O$ and $H$ onto $l$ . The method for drawing perpendiculars from a point $P$ onto a line $p$ is as follows:

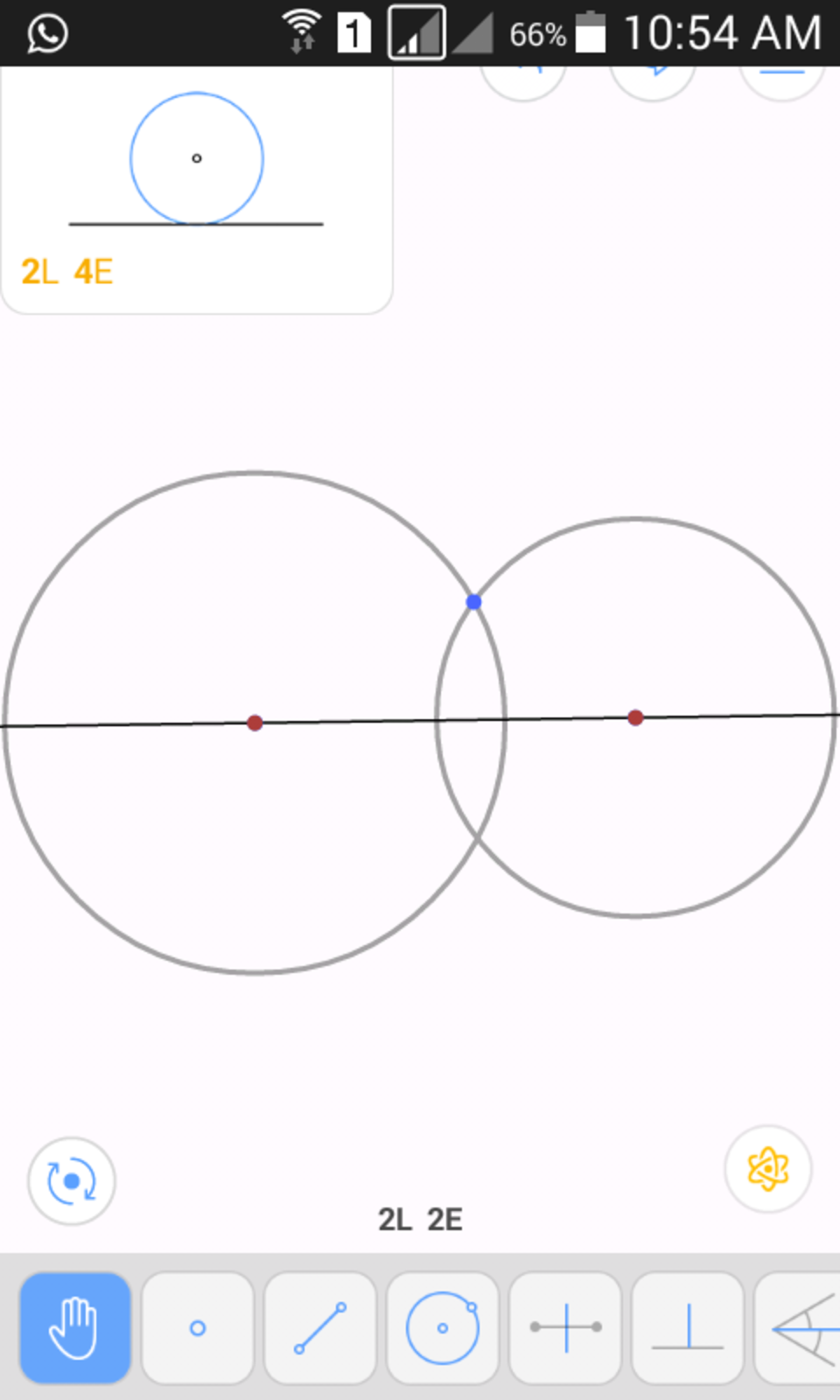
1. From an arbitrary point $Q$ on $p$ , draw a circle passing through $P$ . (1 move)

2. From another arbitrary point $R$ (different from Q) on $p$ , draw a circle passing through $P$ . (1 move)

3. These two circles intersect at $P$ and another point $P'$ . Draw $PP'$ . This is perpendicular to $p$ . (1 move)

Therefore, it takes 3 moves to construct a perpendicular from an exterior point onto a line, so 6 moves will be used to construct the two perpendiculars.

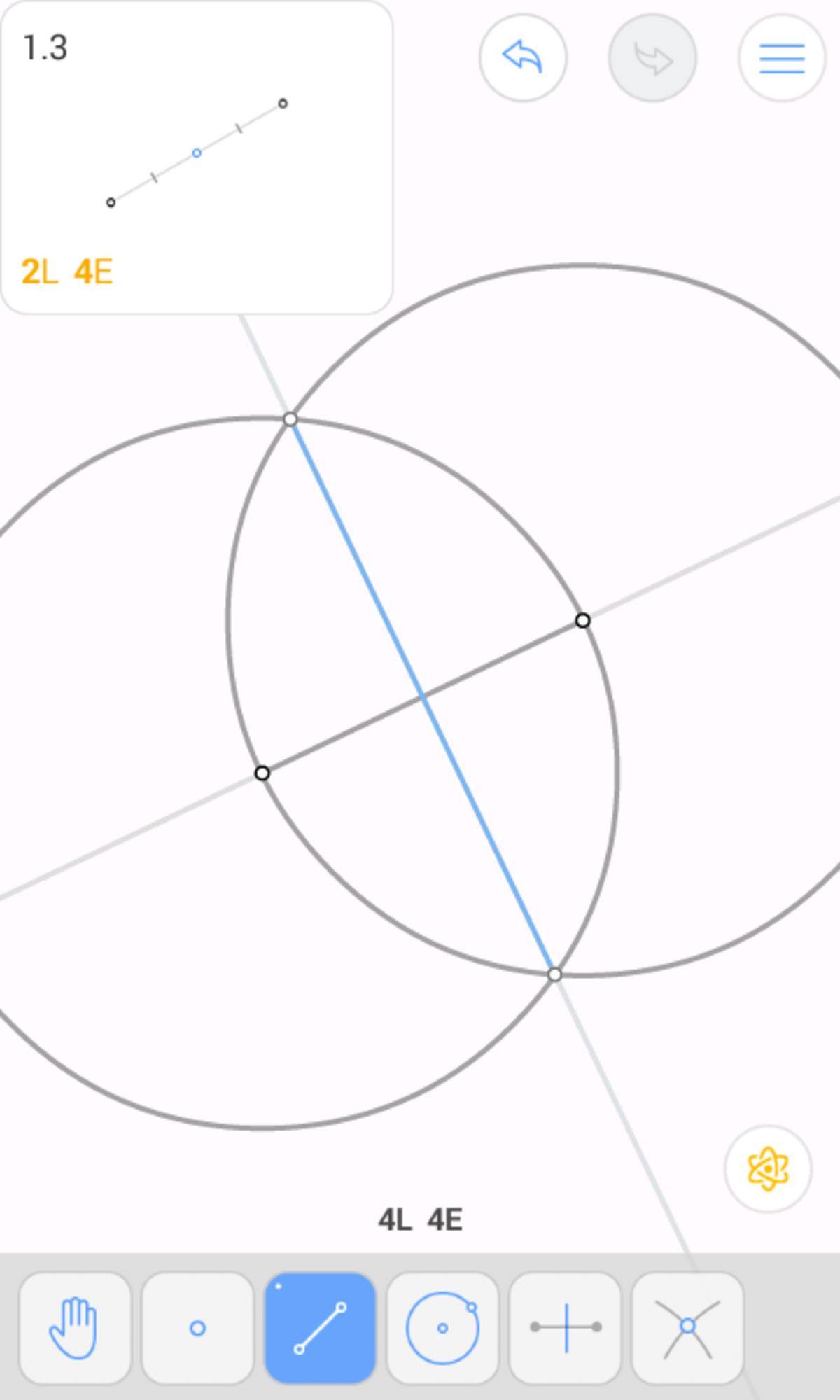
Now, we will locate the centroid (call it $G$ ). By the property of the Euler line, we have $HG : GO = 2 : 1$ . Thus, we will trisect $OH$ partially.

1. Draw $OH$ (and extend it). (1 move)

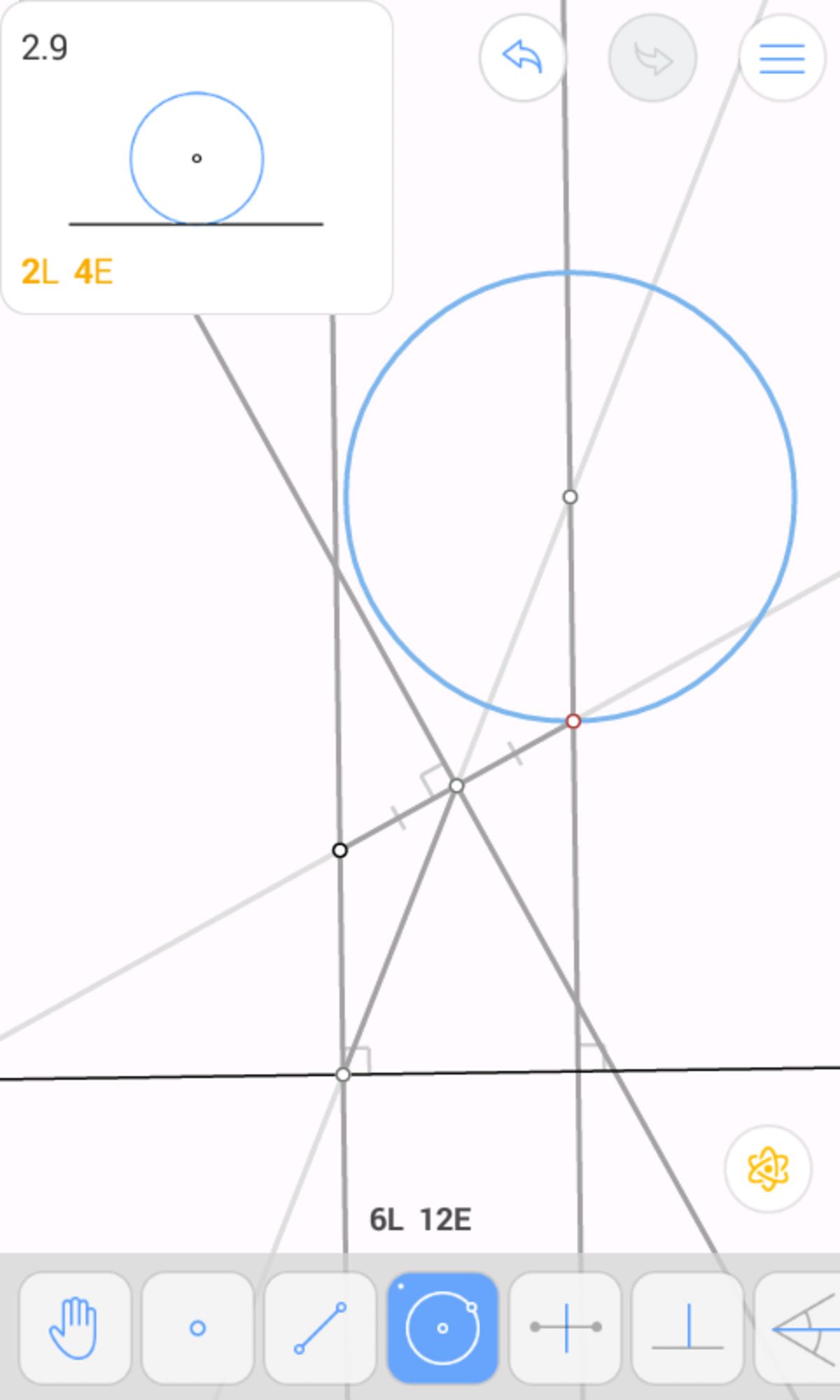
2. Draw a circle centred at $O$ passing through $H$ . Let this intersect $OH$ again at $X$ . (1 move)

3. Draw a circle centred at $H$ passing through $X$ . Let this intersect $OH$ again at $Y$ . (1 move)

4. Draw a circle centred at $Y$ passing through $O$ . Let this intersect the circle centred at $O$ passing through $H$ at $Z$ . (1 move)

5. Draw a circle centred at $Z$ passing through $O$ . This intersects $OH$ again at $G$ . (1 move)

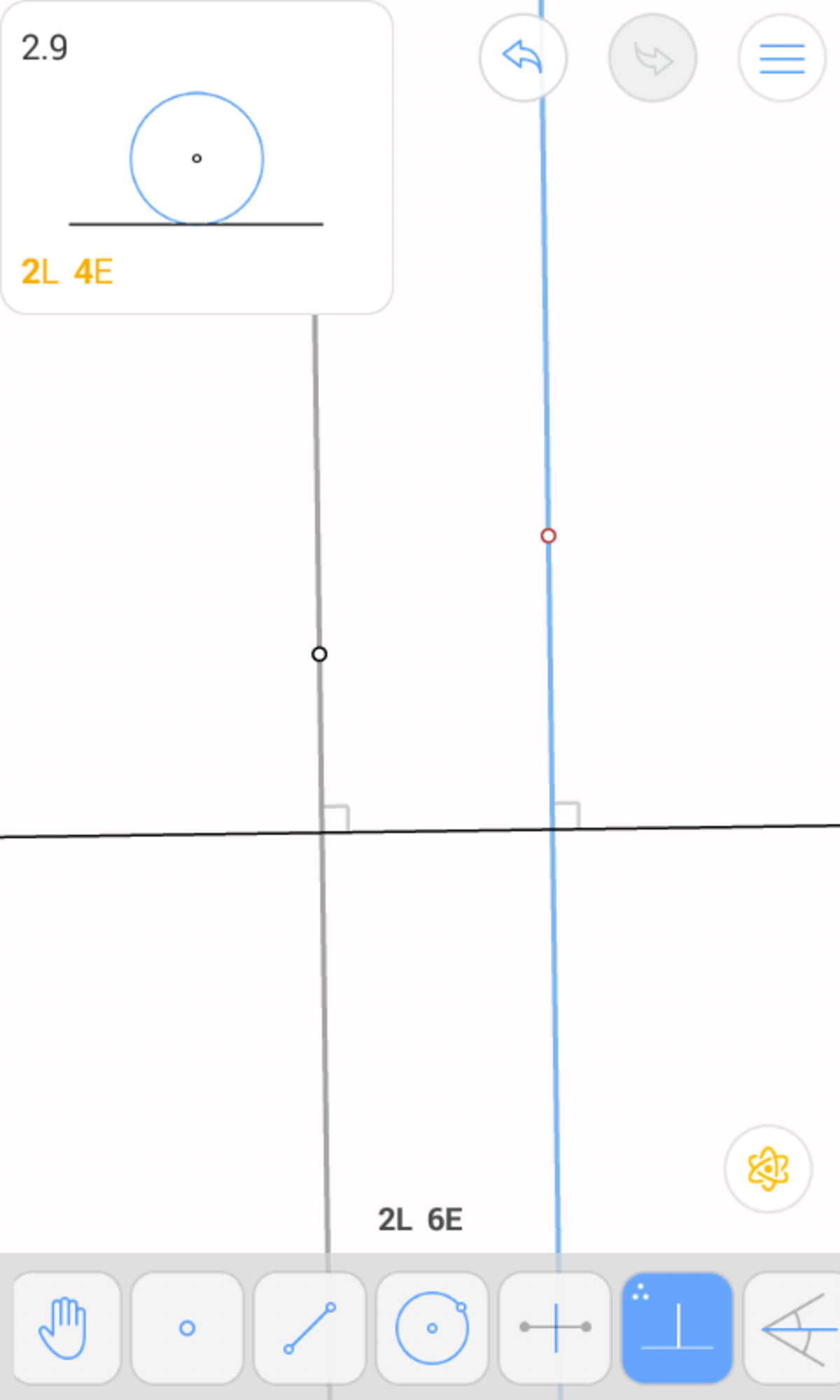
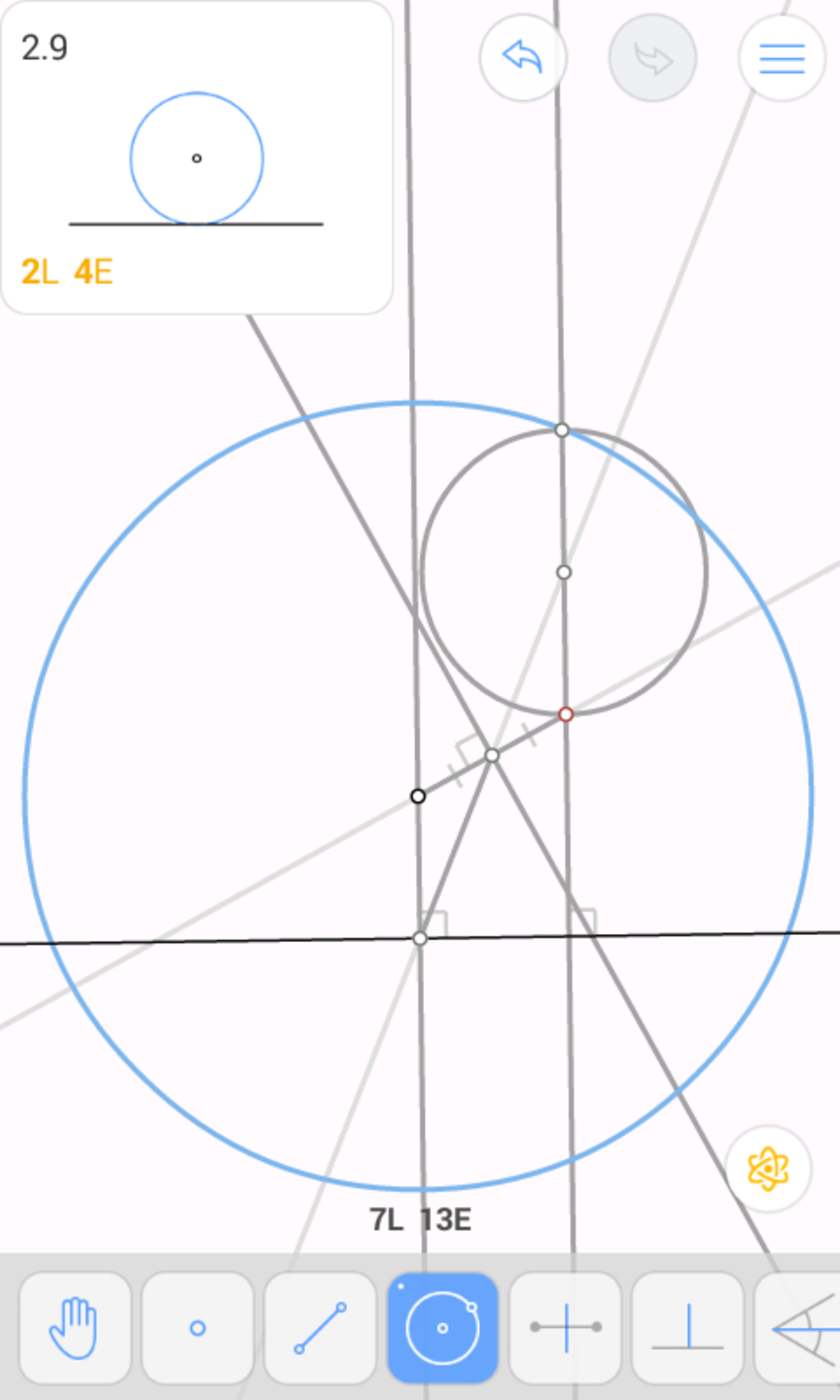
Thus, we have the centroid $G$ located. Let the foot of the perpendicular from $O$ $l$ be called $M$ and the foot of the perpendicular from $H$ to $l$ be called $N$ . Thus, $GM$ is the median of the triangle. We will now locate the apex vertex.

1. Draw $GM$ . Let it intersect $HN$ at $A$ . (1 move)

Thus, we have located the apex vertex. We will finally locate the other two vertices and draw the sides.

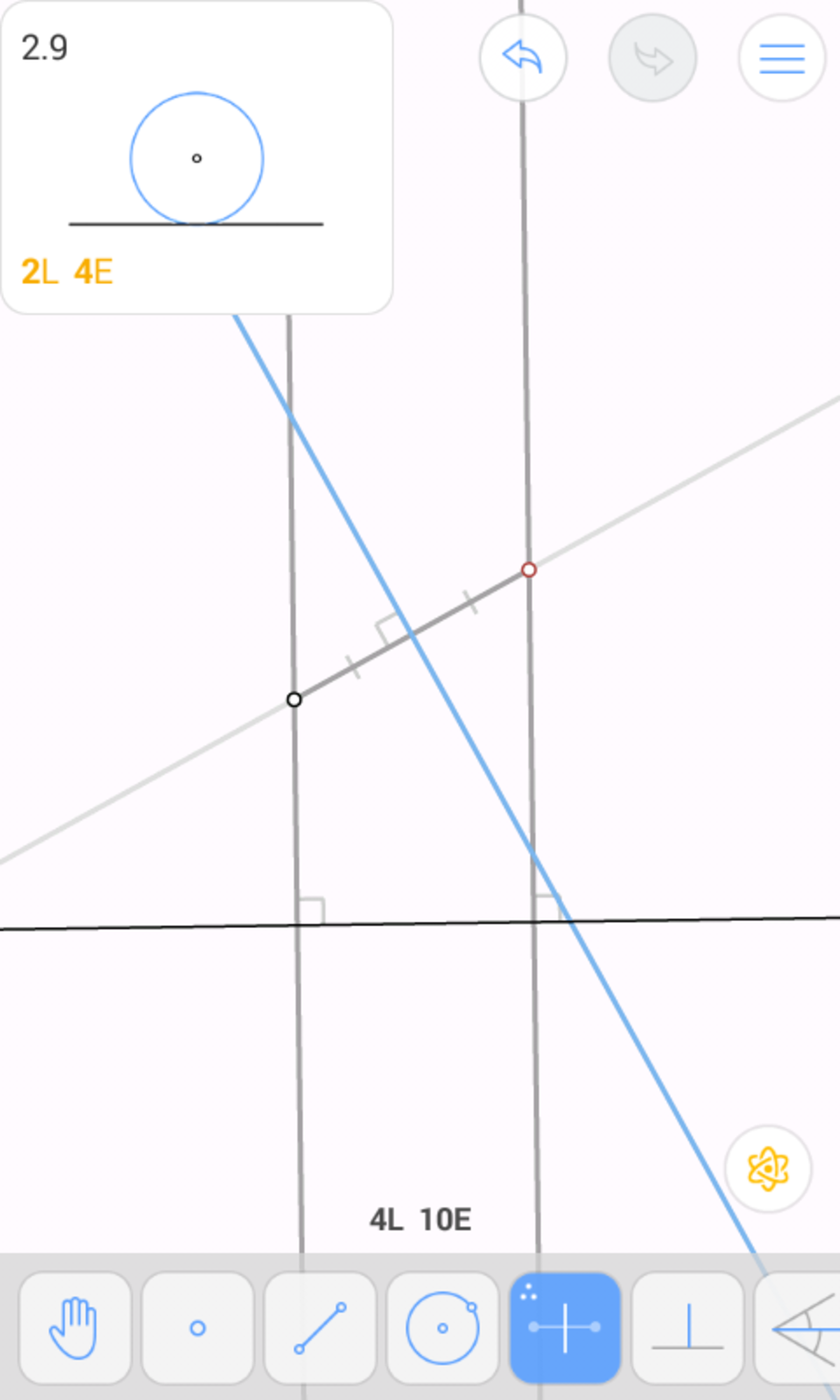
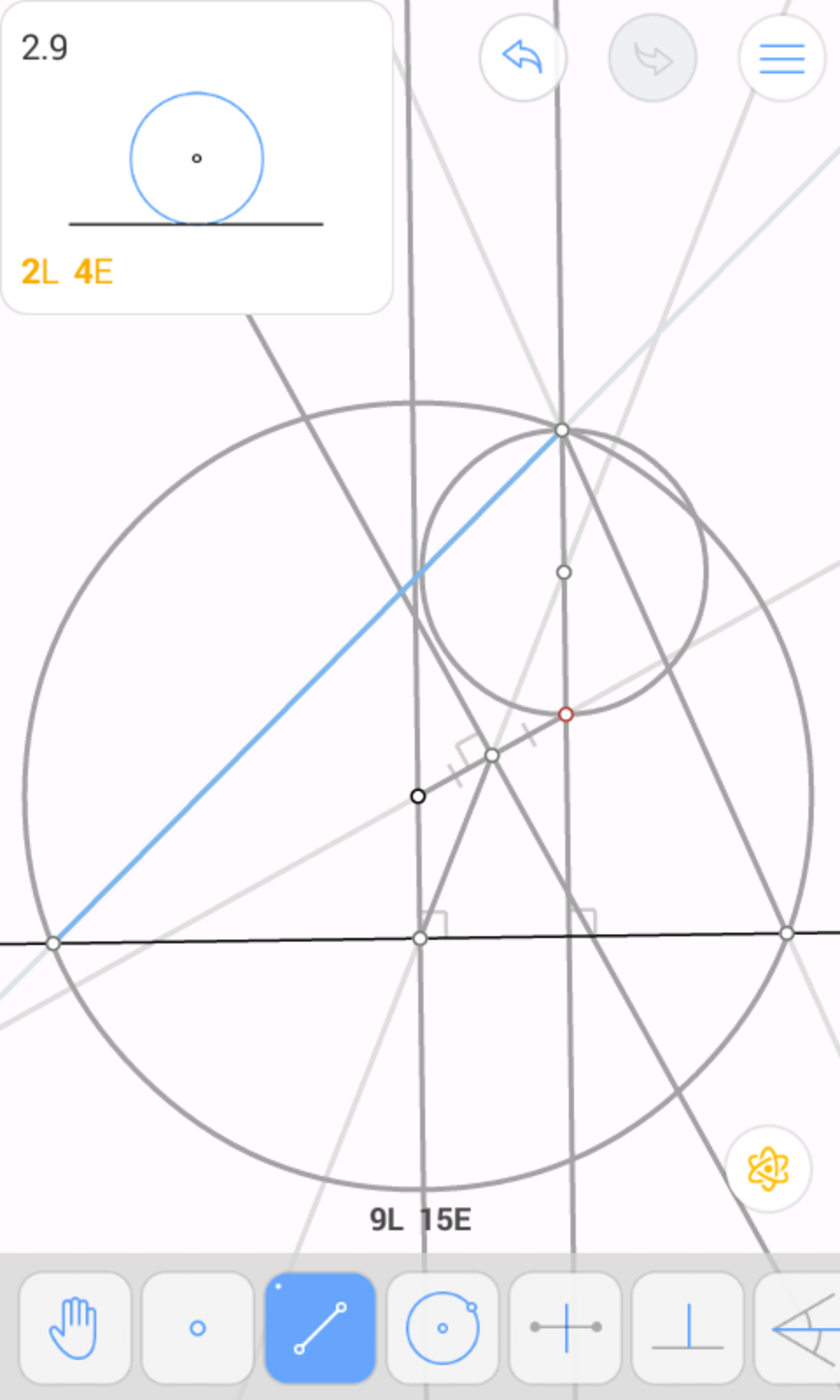
1. Draw a circle centred at $O$ passing through $A$ . Let it intersect $l$ at $B$ and $C$ . (1 move)

2. Draw $AB$ and $AC$ . (2 moves)

Thus, we have drawn the triangle, and it took 6+5+4=15 moves.

---

Jon Haussman has also got 15 moves:

Construct $M$ and $N$ as usual; this takes 6 moves. This construction also gives us line $HN$ .

$\bullet$ Draw the circle centred at $H$ with radius $HO$ . (1 move)

$\bullet$ Draw the circle centred at $O$ with radius $HO$ . (1 move)

$\bullet$ Draw the line $HO$ . (1 move)

$\bullet$ Let the two circles just drawn intersect at $X$ and $Y$ . Draw $XY$ , and let it intersect $HO$ at $P$ . Then $P$ is the midpoint of $HO$ . (1 move)

$\bullet$ Draw line $MP$ , and let it intersect line $HN$ at $Q$ . (1 move)

$\bullet$ Draw the circle centred at $Q$ , and let it intersect line $HN$ at $H$ and $A$ . Then $A$ is a vertex of the triangle we seek. (It is easy to see that $AH = 2MO$ , which is what we want.) (1 move)

$\bullet$ Draw the circle centered at $O$ with radius $OA$ ; let this circle intersect line $l$ at $B$ and $C$ . (1 move)

$\bullet$ Draw lines $AB$ and $AC$ . (2 moves)

The total is 15 moves.

$A$ $self$ $explaining$ $solution$ $without$ $words$ . $So$ $Done$ $in$ $15$ $elementary$ $constructions$ .