A geometry problem by Ronak Singha

Geometry Level 3

Point A is inside the square BCDE whose side length is 20. The length of AB is 9 and the length of AE is 13. Find x the length of AC.

Take the approximate value


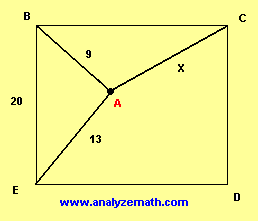
The answer is 17.4.

Ronak Singha by Ronak Singha , 27, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Nguyen Thanh Long
Jul 23, 2015

Applying Heron for triangles ABE theory we have: denote: P = A B + B E + A E 2 P=\frac{AB+BE+AE}{2} [ A B E ] = P × ( P − A B ) × ( P − B E ) × ( P − A E ) [ABE] = \sqrt{P \times (P-AB) \times (P-BE) \times (P-AE)} Denote AH is foot of the line goes through B and orthogonal with BE. → A H = 2 × [ A B E ] B E \rightarrow AH=\frac{2 \times [ABE]}{BE} A C = ( 20 − A H ) 2 + ( 9 2 − A H 2 ) = 17.4 AC = \sqrt{(20-AH)^2+(9^2-AH^2)}=\boxed{17.4}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...