A geometry problem

image

From this image we can see that the blue region is half of the red region in terms of area.

Therefore the area of the red region is 10

The diameter of a regular hexagon is twice its side length, (since a regular hexagon is composed of $6$ identical equilateral triangles).

Thus the top red triangle, having the same height as the blue triangle but half the base length, has an area of $2.5$ . By symmetry, the lower red isosceles trapezoid then has area $5 + 2.5 = 7.5$ , making the area of the red region $2.5 + 7.5 = \boxed{10}$ .

Let the sides of the hexagon be $a$ . We note that the hexagon is made up of six equilateral triangles with side $a$ . The blue area has the area of two of these equilateral triangles and is 5, the red area has the area of four equilateral triangles and therefore its area $=\boxed{10}$ .

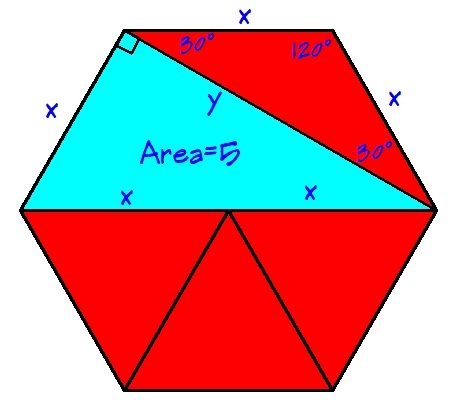By pythagorean theorem, we have $y=\sqrt{(2x)^2-x^2}=\sqrt{4x^2-x^2}=\sqrt{3x^2}=x\sqrt{3}$

The area of the blue region is $5$ , thus

$5=\dfrac{1}{2}(xy)$

$10=x(x\sqrt{3})$

$x^2=\dfrac{10}{\sqrt{3}}$

The area of a regular hexagon is given by $A_H=\dfrac{3}{2}\sqrt{3}x^2$ where $x$ is the side length. Hence

$A_H=\dfrac{3}{2}\sqrt{3}\left(\dfrac{10}{\sqrt{3}}\right)=15$

Therefore, the area of the red region is

$A_R=A_H-A_B=15-5=$ $\boxed{10}$

the red areas are twice the blue area, merge the red, you'll find 10

blue region is 1/3 of the total area of the polygon, that's it