A geometry problem by Rudresh Tomar
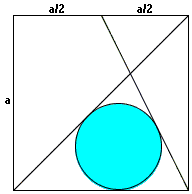 A triangle is formed by a line that joins the base of a square with the midpoint of the opposite side and a diagonal. Find the radius of the inscribed circle.
A triangle is formed by a line that joins the base of a square with the midpoint of the opposite side and a diagonal. Find the radius of the inscribed circle.
Side of square a = 25
The answer is 6.20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the triangle be △ A B C , with A , B and C be the bottom left, bottom right and top vertices respectively. Let the centre of the inscribed circle be O and the point it touches A B be P , its radius be r and A P be x .
Since O is the meeting point of the angle divisors of ∠ C A B and ∠ C B A . Let 2 1 ∠ C B A be θ . Then we have:
tan 8 π = x r tan θ = 2 5 − x r
⇒ x + ( 2 5 − x ) = 2 5 = tan 8 π r + tan θ r ⇒ r = tan 8 π 1 + tan θ 1 2 5
Now we have
tan 4 π = 1 − tan 2 8 π 2 tan 8 π = 1 ⇒ tan 2 8 π + 2 tan 8 π − 1 = 0 ⇒ tan 8 π = 2 − 1
Similarly, tan 2 θ = 2 ⇒ tan 2 θ + tan θ − 1 = 0 ⇒ tan θ = 2 5 − 1
Therefore, r = 2 − 1 1 + 5 − 1 2 2 5 ≈ 6 . 2 0