A geometry problem by Sakanksha Deo

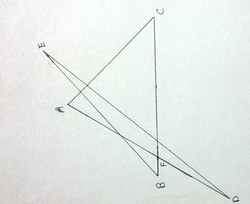Write a solution. $\angle{A} + \angle{C} + \angle{AFC} = 180$ ... (1)

$\angle{B} + \angle{D} + \angle{E} = \angle{BFD} = \angle{AFC}$ ... (2)

From (1) and (2) , we get ,

$\angle{A} + \angle{B} + \angle{C} + \angle{D} + \angle{E} = \boxed{180}$

Apply exterior angle property in two triangles. Then use angle sum prop.

Method 1:

Let $1,2,3,4$ and $5$ be the angles of the irregular pentagram .

By the Exterior Angle Theorem , $\angle FGD=1+3$ because $\angle 1$ and $\angle 3$ are remote angles. It follows that $\angle GFD=2+4$ since it is an exterior angle with remote angles $2$ and $4$ . The sum of the interior angles of $\triangle FGD=1+3+2+4+5=180^\circ$ . But these are the angles of the pentagram. Hence, the sum of the angles of the pentagram is $\boxed{180^\circ}$ .

Method 2:

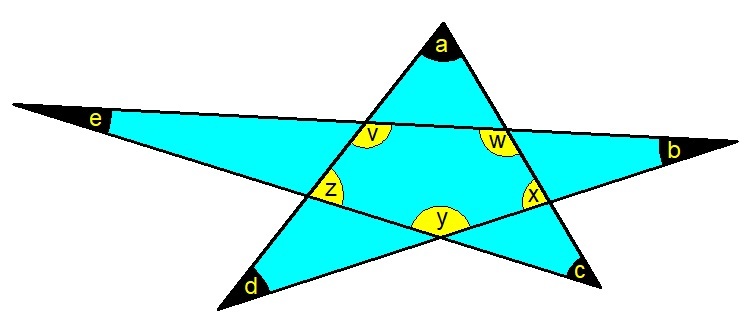Consider the diagram on the above.

$v=180-(b+d)$

$w=180-(c+e)$

$x=180-(a+d)$

$y=180-(b+e)$

$z=180-(a+c)$

We know that $v+w+x+y+z=540$ . So

$180-(b+d) + 180-(c+e) + 180-(a+d) + 180-(b+e) + 180-(a+c) = 540$

$900 - 2(a+b+c+d+e)=540$

$900-540=2(a+b+c+d+e)$

$360=2(a+b+c+d+e)$

$a+b+c+d+e=$ $\boxed{180}$