Area Of The Medial Triangle
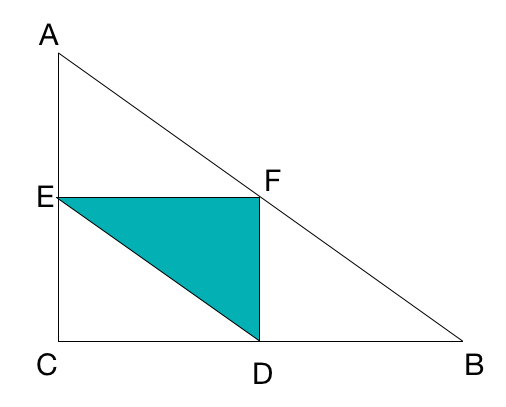
Let D , E , F be the midpoints of the sides of △ A B C .
The area of △ A B C is X and the area of △ D E F is Y .
Enter your answer as Y X .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Thanks for sharing multiple approaches. The similar triangle argument should be easily understood :)
Let A C = a and C B = b so the area of △ A B C = X = 2 a b and △ D E F = Y = 8 a b
Then Y X = 8 a b 2 a b = 4
You are assuming the triangle is right-angled. The result applies to any triangle.
Relevant wiki: Area of Triangles - Problem Solving - Medium
I will offer a couple of different methods to solve this problem. For notation purposes let [ △ A B C ] denote the area of △ A B C .
Method 1: Areal/Barycentric Coordinates
A , B , C have areal coordinates ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 )
D , E , F will have the areal coordinates ( 0 , 2 1 , 2 1 ) , ( 2 1 , 0 , 2 1 ) , ( 2 1 , 2 1 , 0 ) .
The area of a triangle from its areal coordinates can be calculated from the determinate of the matrix of its coordinates so:
Y X = ∣ ∣ ∣ ∣ ∣ ∣ 0 0 . 5 0 . 5 0 . 5 0 0 . 5 0 . 5 0 . 5 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 0 0 0 1 0 0 0 1 ∣ ∣ ∣ ∣ ∣ ∣ = 4 1 1 = 4
Method 2: Similar Triangles.
Let D , E , F be the midpoints of A B , A C , B C respectively.
An enlargement about A of scale factor 2 carries D to B and E to C . It therefore follows that △ A D E ≅ △ A B C .
As the sides are in ratio 1 : 2 it follows [ △ A B C ] [ △ A D E ] = 4 1 ⟹ [ △ A D E ] = 4 [ △ A B C ] .
We have similar results for △ B D F and △ C E F .
[ △ B D F ] + [ △ C E F ] + [ △ A D E ] = 4 3 [ △ A B C ]
[ △ D E F ] = [ △ A B C ] − ( [ △ B D F ] + [ △ C E F ] + [ △ A D E ] ) = 4 [ △ A B C ]
We therefore have Y X = 4 1 1 = 4