A geometry problem by Soham Chitnis
Points B, D, and J are midpoints of the sides of right triangle ACG. Points K, E, I are midpoints of the sides of triangle JDG, etc. If the dividing and shading process is done 100 times (the first three are shown) and AC=CG=6
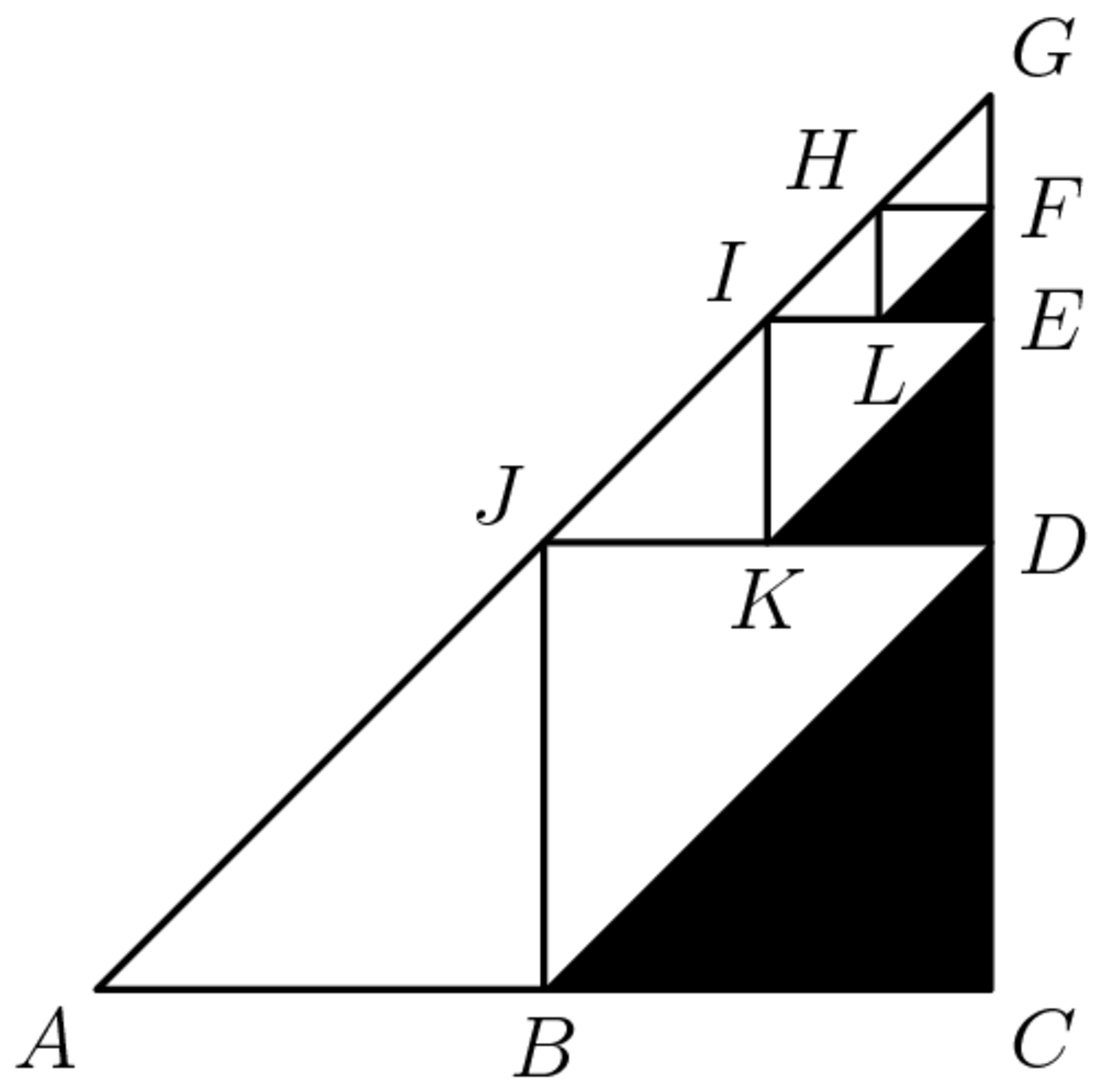 , then the total area of the shaded triangles is nearest
, then the total area of the shaded triangles is nearest
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 9 + 8 9 + 3 2 9 + 1 2 8 9 + . . .
This is the sum of a geometric series with first term a = 2 9 and common ratio r = 4 1 .
The sum of an infinite geometric series with ∣ r ∣ < 1 is S ∞ = 1 − r a = 1 − 4 1 2 9 = 2 9 ⋅ 3 4 = 6 , giving an answer of option A i.e 6