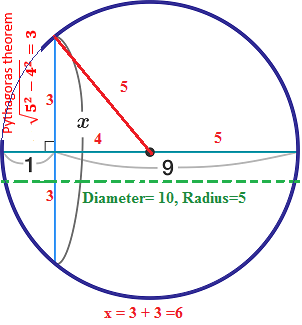
Right angle triangles are great!
In a circle, a chord divides the diameter perpendicularly into lengths of 1 and 9. What is the length of the chord?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
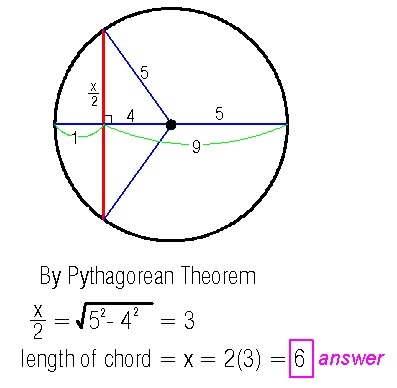
Be careful when claiming the units to be cm. They're not known in this case.
Nice solution. Thank you
you're welcome ..
Precise and clear explanation.
3-4-5 is the first Pythagorean triad. It is said that architects in the ancient Egypt and Babylon used ropes with these measures to draw square angles on site.
Log in to reply
Makes sense, since it is the smallest Pythagorean triple. I find it interesting that people knew about this special triangle so many thousand years ago.
This solution is the best so far. It only uses pythagorean theorem which is very basic. We don't need to compute for 2 x , because the triangle formed is a 3 − 4 − 5 special right triangle. So without computation, 2 x = 3 . That means that x = 6
Using the
intersecting chords theorem
,
1
×
9
=
(
2
x
)
2
⟹
2
x
=
3
⟹
x
=
6
.
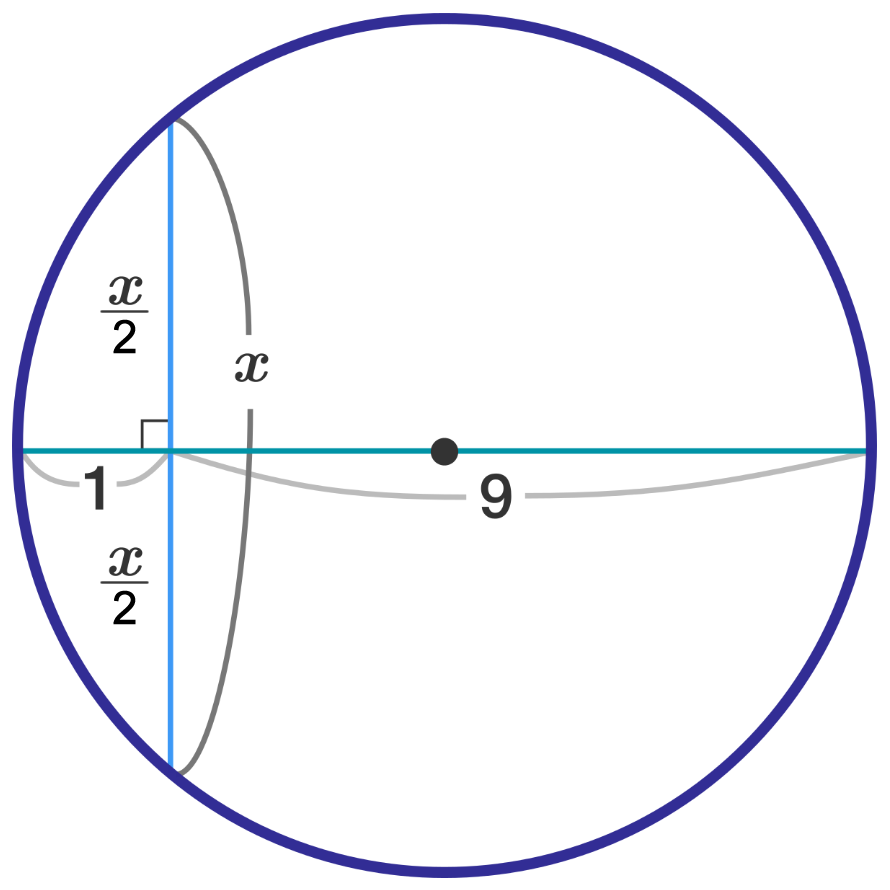
Ah, Intersecting chords theorems is my first favorite circles theorem that I've learned on my own. So nostalgic~~
On the other hand, I can't seem to find the proof anymore. Dang it. Let me see if I can prove it again...
Neat solution as usual, Dan!
Log in to reply
Thanks!! I think we can use the circle theorem of angles in the same segment and similar triangles to get there!
Using the intersecting chords theorem is also good, but not all problem solvers are familiar with the theorem. They are more familiar with the pythagorean theorem. Actually, I used the pythagorean theorem to solve this.
Log in to reply
Of course, just an alternative method to the one already posted.
I think ptolemy is a better terminology than intersecting chords theorem.
Let point where chord touches circle be C. The ends of the horizontal line are A and B.
Since AB passes through center of circle it is a diameter and ABC is right triangle with right angle at C.
Distance from AB to C is X. By Pythagorean's theorem 1^2 + X^2 = AC^2, and 9^2 +X^2 = BC^2.
AC^2 + BC^2 = 10^2 = 100 so 1^2 + X^2 + 9^2 + X^2 = 100.
2*X^2 + 82 = 100
2*X^2 = 18
X^2 = 9
X = 3 so 2*X = 6
Not as compact as others but when I drew the picture the large right triangle is what I saw.
Interesting approach, Roger. Did you notice that X = 3 is the geometric mean of 1 and 9? We can find the geometric mean of any two numbers geometrically using this construction!
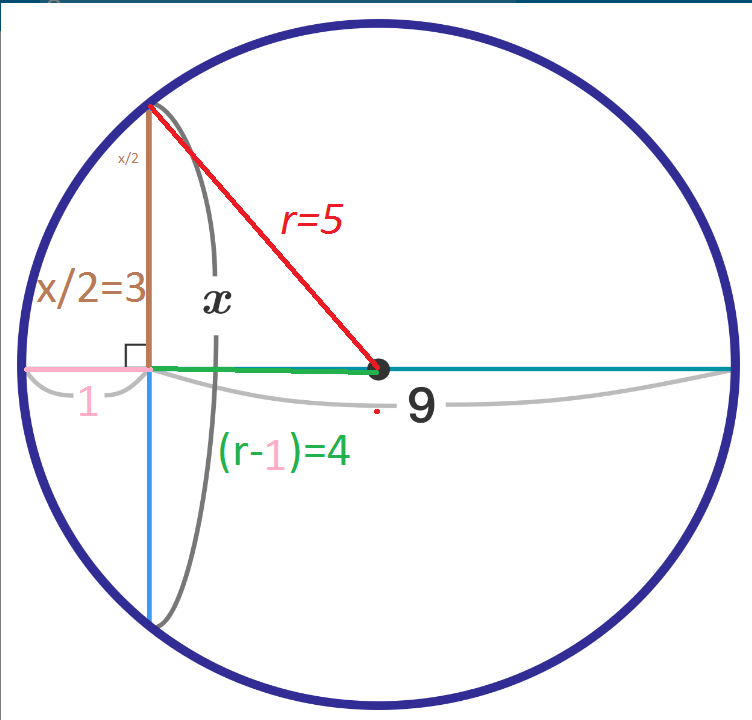
used pythogorean theorem i used colors because it might help u understand better, so u should focus on it.
I like the picture. Mirrors my thinking.
The longest possible HORIZONTAL distance from the chord to a point on the boundary of circle is on the diameter of circle. So the diameter of the circle is divided into lengths 9 cm and 1cm by the vertical chord.
Step 1:
Draw the circle, chord and label the lengths.
Step 2:
Let the length of the chord be X.
The radius of the circle is 5. So, one can form a right angle triangle with height = 2 X , base = 5-1= 4 and hypotenuse = 5.
Step 3:
Use Pythagoras theorem to get:
2 X = 5 2 − 4 2 = 2 5 − 1 6 = 9 = 3
Step 4:
Length of the chord, X = 3 ∗ 2 = 6
There is one more way to find the length of any chord perpendicular to diameter. Given a horizontal diameter, it will always bisect a vertical chord (through it) at any position. If a chord, perpendicular to diameter of length d cm, cut the diameter into lengths x cm and (d-x) cm, then the length of that chord is double of ( d − x ) ∗ ( x )
Nice problem, Stuti. How do we know that the diameter bisects the chord?
Log in to reply
Thanks, The horizontal diameter of the circle will always divide all the vertical chords into two equal lengths because of symmetry. In general, if any diameter and chord are perpendicular, that diameter will always bisect the chord. Given any chord, one can construct a diameter such that it bisects that chord by finding the centre of chord and drawing a perpendicular line passing through the centre of chord and circle and extending it so that it becomes a diameter. In fact, a diameter is a also chord but it passes through the centre of circle. Diameter will bisect any non diameter chord if and only if it is perpendicular to it.
Log in to reply
Thanks for explaining, this makes it clear. If the radius is perpendicular to a chord, then the chord is being bisected.
The solution can also be found using the equation for a circle centered at the origin: y 2 + x 2 = r 2 [note x here is referring to the coordinates, not the length of the chord]. Here, r = 5 , and where the chord intersects the diameter, x = − 4 . Substituting and solving for y , we get y = 3 , which is half the length of the chord. So the answer is 6.
Coordinate geometry solution is always comes in handy, doesn't it?
How did we deduce that the segment of length 9 is broken into pieces of 5 and 4?
Log in to reply
The diameter is 9+1=10. I mentioned it in the green color.
All non-degenerate triangles inscribed in a circle with the diameter as one side are right triangles. The chord in this diagram is the altitude of said right triangle. From the proportionality of similar triangles, it is straightforward to show the the altitude is the geometric mean of the two sections of the diameter. 1 * 9 = 3^2, and the chord is double the altitude, 2 * 3 = 6.
Nice use of similar triangles, Tom. All three triangles that are formed are similar to each other!
Using ptolemy theorem allows us to know that 9 = 0.25x^2 Now, we need to solve for x which is 6
Use the geometric mean to find the half of the chord .x/2= sqrt of 1 times 9 ......x/2=3 ... × = 6 .