A geometry problem by Suvajyoti Barman
Geometry
Level
3
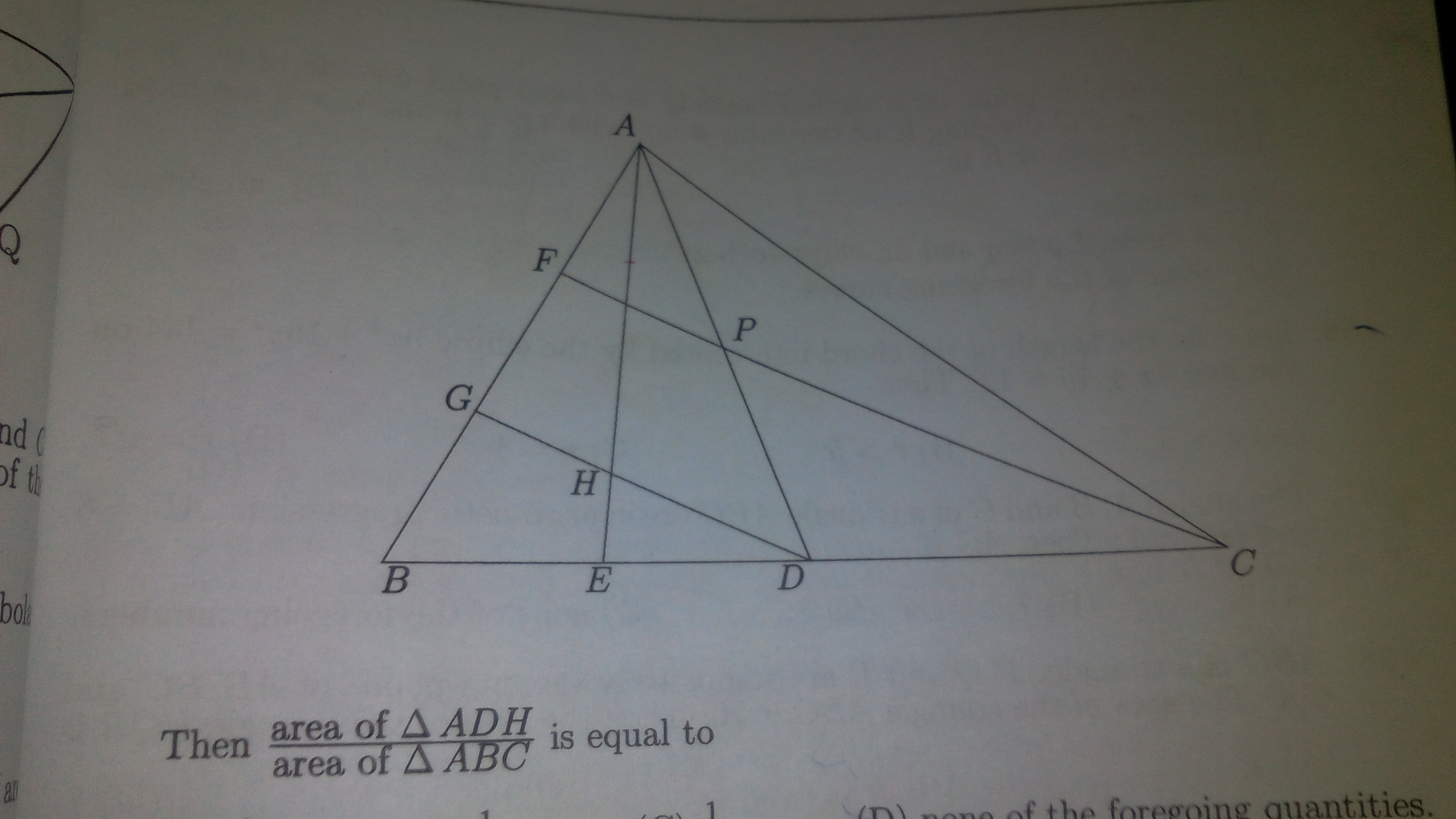
In the given figure,BD=CD,BE=DE,AP=PD DG||CF. Find area of ADH/area of ABC
1/3
1/5
1/4
none of the rest
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Looking purely at the lengths of the bottom segments, AD cuts the entire triangle in half and AE cuts one of those halves in half. This makes makes triangle AED 1/4th the original triangle, but we're looking for ADH, which is clearly less than that amount. This at least rules out 1/4 and 1/3 as answers.
I'm not sure how to reach 1/5 as the correct answer, but for that to be the case, triangle HED has to be 1/20th of the original full triangle since 1/5 + 1/20 = 1/4.
My reasoning may be off but there may be another way to reach 1/5 if it can be determined that the triangle formed by A, P and the unlabeled point they touch is 1/20 because ADH is a similar triangle that is 4 times as large (it's side lengths are doubled).
We also have a lot of information about the side lengths of ADH. HE is the only length we don't yet have a relationship established with some other part. There may be a way to calculate the area as a proportion of the area of AED which we know is 1/4.