A geometry problem by Swapan Bagchi
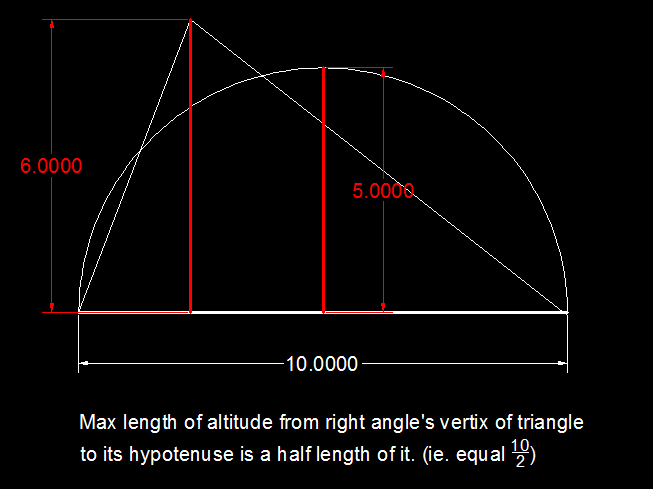
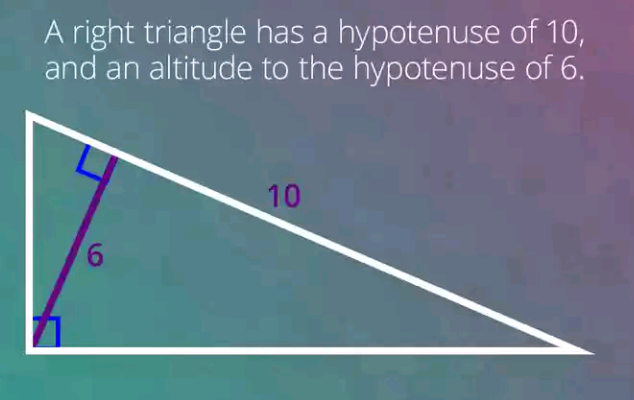 Is the given triangle possible?
Is the given triangle possible?
If 'yes' enter the area of the given triangle or if 'no' then
enter 0 and also explain your reasoning to the same in discussions.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Let the sides of the triangle be x and y . By considering the area of the triangle we get:
2 x y = 2 1 0 × 6 ⇒ x y = 6 0
Also because the triangle is right-angled we have:
x 2 + y 2 = 1 0 2 ⇒ x 2 + y 2 = 1 0 0
Now by GM-QM inequality we have:
x y ≤ 2 x 2 + y 2
Putting in our values for x y and x 2 + y 2 we get:
6 0 ≤ 2 1 0 0 ⇒ 6 0 ≤ 5 0 ⇒ 6 0 ≤ 5 0
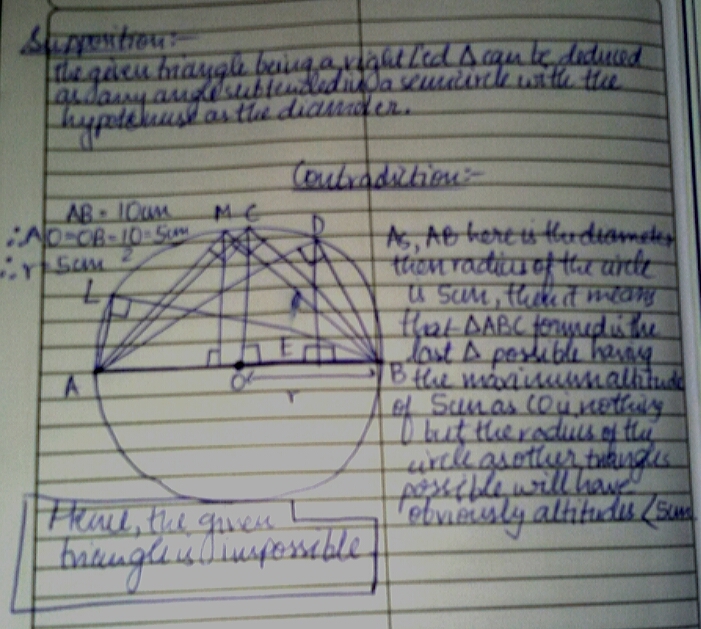
This is clearly a contradiction so no such triangle exists.
Moderator note:
Well explained.
If we divide the hypothenuse into lengths of x and 1 0 − x , then by Geometric Means:
x 6 = 6 1 0 − x ⇒ 3 6 = − x 2 + 1 0 x ⇒ x 2 − 1 0 x + 3 6 = 0 ⇒ x = 2 1 0 ± 1 0 2 − 4 ( 1 ) ( 3 6 ) = 2 1 0 ± − 4 4 ⇒ x = 5 ± 1 1 i
which means this right triangle configuration is impossible since x ∈ / ( 0 , 1 0 ) .
Q . E . D .
If a right triangle has a hypotenuse of 10, it means the other sides should be 6 and 8. Thus, the area should be 24. with the given dimensions of the altitude and the hypotenuse the area is 30.
Hana , if the hypotenuse is 10 it means that perp.^2 + base^2 should be 100 . In this case there are not only 6 and 8 but also pairs like 9 1 , 3 or 4 5 , 5 5 and so on. It need not necessarily be 6, 8.
Log in to reply
ok, I saw your solution, I am going to dig into it, see what you did.