A geometry problem by Tanishq Varshney
Consider a point P on the line y = x and two fixed point A ( 3 , 4 ) and B ( 6 , 1 3 ) .Then find P such that P A + P B is minimum.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Elaborate it
I have tried this problem out in two different ways: Firstly graphically. The locus of points that have PA+PB constant is an ellipse with points A and B as its focuses. To minimise the size of PA+PB we need to find the smallest ellipse that will just touch the line y=x; Constructing this graphically in a CAD package shows the tangent being very close to (17/4,17/4).
Secondly algebraically: since x=y on the line we can substitute x for y and get;
PA + PB is ( x − 3 ) 2 + ( x − 4 ) 2 + ( x − 6 ) 2 + ( x − 1 3 ) 2
differentiating the above, then considering only the numerator, gives
( x − 7 ) 2 x 2 − 3 8 x + 2 0 5 + ( x − 1 9 ) 2 x 2 − 1 4 x + 2 5
this must be zero at the point where AP+BP is a minimum (or maximum), and it can be solved numerically to be exactly 17/4.
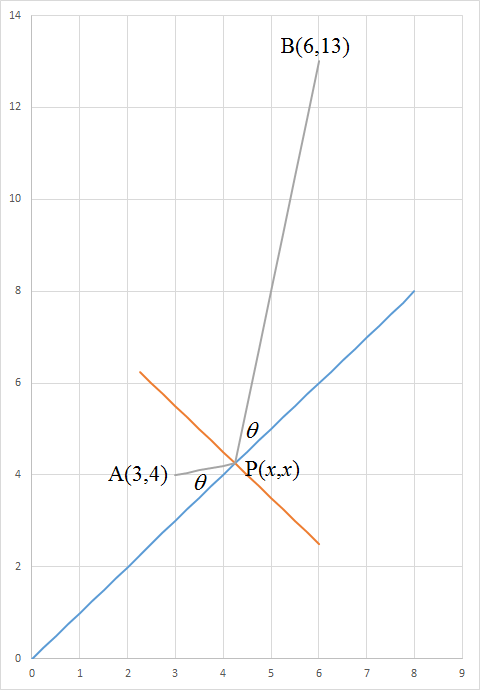
Since P is on the line y = x , let its coordinates be P ( x , x ) . The shortest P A + P B is when P A is an incident light ray and P B the reflected light ray at point P on the mirror y = x as shown in the figure. Since the incident angle equals to the reflective angle, the angle P A makes with y = x is the same as P B makes with y = x and equals to θ . Then the gradients of P A and P B , m A and m B respectively are given by:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ m A = tan ( 4 π − θ ) = x − 3 x − 4 m B = tan ( 4 π + θ ) = x − 6 x − 1 3 ⟹ θ = 4 π − tan − 1 ( x − 3 x − 4 ) ⟹ θ = tan − 1 ( x − 6 x − 1 3 ) − 4 π
⟹ 4 π − tan − 1 ( x − 3 x − 4 ) 2 π − tan − 1 ( x − 3 x − 4 ) cot − 1 ( x − 3 x − 4 ) tan − 1 ( x − 4 x − 3 ) x − 4 x − 3 ( x − 3 ) ( x − 6 ) x 2 − 9 x + 1 8 8 x ⟹ x = tan − 1 ( x − 6 x − 1 3 ) − 4 π = tan − 1 ( x − 6 x − 1 3 ) = tan − 1 ( x − 6 x − 1 3 ) = tan − 1 ( x − 6 x − 1 3 ) = x − 6 x − 1 3 = ( x − 1 3 ) ( x − 4 ) = x 2 − 1 7 x + 5 2 = 3 4 = 4 1 7
Therefore, P ( 4 1 7 , 4 1 7 ) .
take the image of point p in the line y=x which comes out to be A (4,3) using congruent triangles u can see that PA=PA Now take a point p ony=x say (t,t) from the slope we have slope of A B=PB solve for t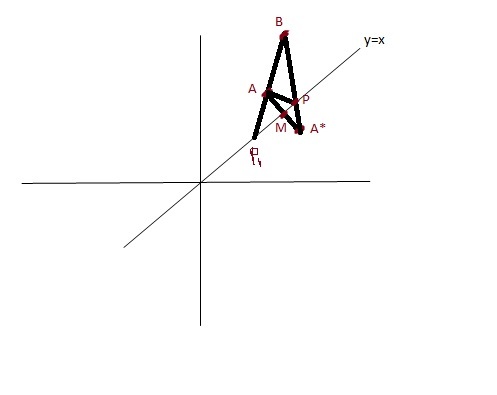 A
is the image of A in y=x. we cannaot take point P1 as PA+PB will not be minimum. also tr(APM) is congruent to tr(A*PM) by SAS RULE.
A
is the image of A in y=x. we cannaot take point P1 as PA+PB will not be minimum. also tr(APM) is congruent to tr(A*PM) by SAS RULE.