SAT Properties of Triangles
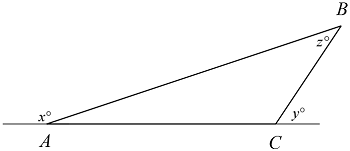
In the figure above, which of the following is the value of
expressed in terms of
and
(A)
(B)
(C)
(D)
(E)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Correct Answer: C
Solution 1:
Tip: The measure of an exterior angle of a triangle equals the sum of the measures of the two non-adjacent interior angles.
∠ B A C and ∠ x are supplementary angles. Therefore, their measures add to 1 8 0 ∘ and
m ∠ B A C = 1 8 0 − x .
∠ y is exterior, and therefore its measure equals the sum of the measures of the two remote interior angles:
y y x + y − 1 8 0 = m ∠ B A C + z = 1 8 0 − x + z = z
Solution 2:
Tip: The measures of the angles in a triangle add to 1 8 0 ∘ .
∠ B A C and ∠ x are supplementary angles. ∠ B C A and ∠ y are supplementary angles too. From the definition of supplementary angles, it follows that
m ∠ B A C = 1 8 0 − x and
m ∠ B C A = 1 8 0 − y
The measures of the angles in a triangle add to 1 8 0 ∘ . Therefore,
m ∠ A B C + m ∠ B A C + m ∠ B C A m ∠ A B C z z z = = = = = 1 8 0 1 8 0 − m ∠ B A C − m ∠ B C A 1 8 0 − ( 1 8 0 − x ) − ( 1 8 0 − y ) 1 8 0 − 1 8 0 + x − 1 8 0 + y x + y − 1 8 0
Incorrect Choices:
(A)
If you think that x , y , and z add to 180 ∘ , you will get this wrong answer. x and y are exterior, and not interior, angles.
(B)
You will get this wrong answer if in Solution 1 you add 180 to both sides instead of subtract it from both sides, like this:
y x + y + 1 8 0 = 1 8 0 − x + z = z mistake: added instead of subtracted
or if in Solution 2 you add m ∠ B C A to both sides instead of subtract it, like this:
m ∠ A B C + m ∠ B A C + m ∠ B C A = 1 8 0 m ∠ A B C = 1 8 0 − m ∠ B A C + m ∠ B C A mistake: added, instead of subtracted z = 1 8 0 − ( 1 8 0 − x ) + ( 1 8 0 − y )
(D)
If you apply to ∠ z the theorem which states that the measure of an exterior angle in a triangle equals the sum of the measures of the two nonadjacent interior angles, you will get this wrong answer. Note that ∠ z is an interior angle, and ∠ x and ∠ y are exterior angles.
(E)
This wrong choice is the sum of the measures of ∠ B A C and ∠ B C A . It is offered to confuse you.