Hone in all 3 spots
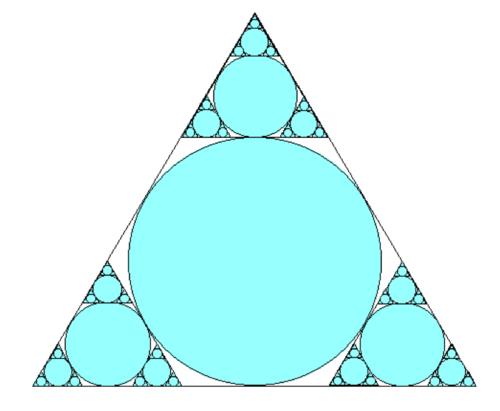 If the pattern of inscribed circles shown in the image above is repeated infinitely, and the side length of the equilateral triangle is
, then find the area of all the circles in terms of
.
If the pattern of inscribed circles shown in the image above is repeated infinitely, and the side length of the equilateral triangle is
, then find the area of all the circles in terms of
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
These two graphics are all we'll need to solve this problem. The picture on the left helps us determine the radius of the largest inscribed circle with the construction of a well placed right triangle. The radius of this largest circle is 6 a 3 , thereby making the area of this circle equal to 1 2 a 2 π .
Now, the graphic on the right shows that the self-similar image of the large fractal is 9 1 the size of the original. However, there are 3 such self-similar images, so the contribution by the next largest circles is 3 1 the first contribution. It turns out that this pattern will continue infinitely, where the next largest circles are 9 1 in size, but are in 3 times the abundance of the previous circles, meaning each area contribution is 3 1 of the previous contribution. This pattern creates a geometric series whose first term is 1 2 a 2 π and whose common ratio is 3 1 . Using the geometric progression sum formula, we find that the total area is equal to
1 − 3 1 1 2 a 2 π = 8 a 2 π