A geometry problem by Tushar Verma
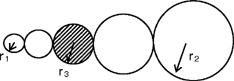 The five circles shown above have two direct common tangents.
If
r
1
=
8
cm,
r
2
=
5
0
cm, find
r
3
.
The five circles shown above have two direct common tangents.
If
r
1
=
8
cm,
r
2
=
5
0
cm, find
r
3
.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This might seem trivial, but could you elaborate as to how you got this result? It would really help a lot! Thank you.
How do you know the circles form a G.P.?
There are 5 circles here.Let us consider the ratio between the radii is p.So we can write 50=8 p p p p,so p=1.58.So r3=8 P P=20
How do you know the circles form a G.P.?
We can imagine that the circles are homothetic transformations onto each other, so they are all similar with a constant ratio, so the radius of the center circle is the geometric mean of that of the outside circles.
{ r ( k ) } , k ∈ N ∪ { 0 } is a G.P.
r ( k ) r ( k + 1 ) = q ,
q constant ratio of the G.P.
r ( k ) r ( k + h ) = q h ; r ( h ) r ( 2 h ) = q h r ( 2 ) r ( 4 ) = q 2 ; r ( 0 ) r ( 2 ) = q 2 r ( 2 ) r ( 4 ) = r ( 0 ) r ( 2 ) ; r ( 2 ) = r ( 4 ) r ( 0 )
r ( 0 ) = r 2 = 5 0 , r 1 = r ( 4 ) = 8 , r 3 = r ( 2 ) , r 3 = r 1 r 2 = 4 0 0 = 2 0
as Hassan said, the radii are in GP..
How do you know the circles form a G.P.?
The geometric mean: sqrt(8 x 50} = sqrt(400) = 20 yay!