A geometry problem by vansh gupta

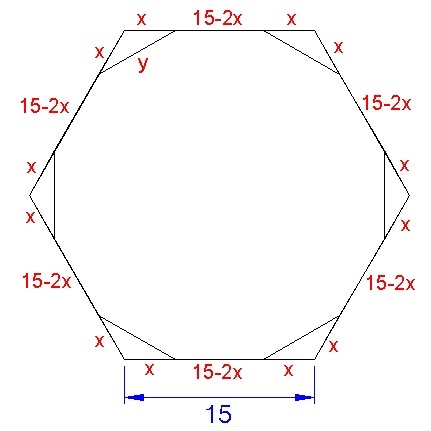We let the amount we cut off the corners be $x$ ,

From my figure, by cosine rule ,

$y^2=x^2+x^2-2(x)(x)(cos~120)$

$y=x\sqrt{3}$

However, $y=15-2x$ , we equate the two equations

$15-2x=x\sqrt{3}$

$x=\dfrac{15}{2+\sqrt{3}}$

It follows that,

$y=x\sqrt{3}=\dfrac{15\sqrt{3}}{2+\sqrt{3}}$

The perimeter of the regular 12 sided polygon is therefore,

$P=12y=12(\dfrac{15\sqrt{3}}{2+\sqrt{3}})=\dfrac{180\sqrt{3}}{2+\sqrt{3}}$

The perimeter of the hexagon is

$P_H=6(15)=90$

Finally, the ratio of their perimeters is

$\dfrac{\frac{180\sqrt{3}}{2+\sqrt{3}}}{90}\approx 0.928$

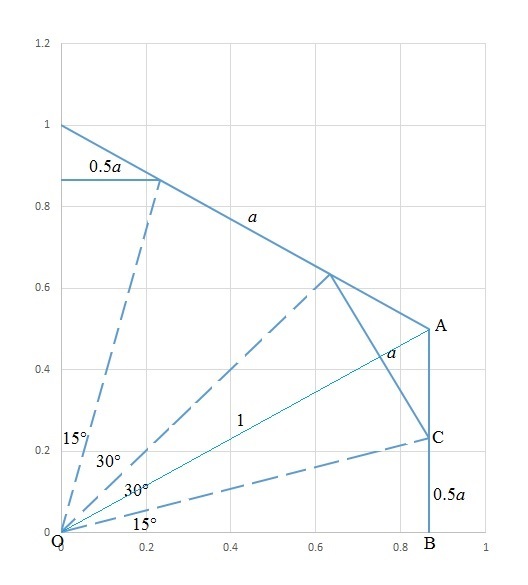
Let the side length of the regular hexagon be 1 (15 cm), then the radius of circumcircle of the hexagon $OA$ is also 1. Let the side length of the regular 12-sided polygon be $a$ . Then we note that:

$\begin{aligned} CB & = OB \tan 15^\circ \\ \frac a2 & = OA \cos 30^\circ \tan 15^\circ \\ a & = 2 \cos 30^\circ \tan 15^\circ \end{aligned}$

Therefore, the ratio of the perimeter of the 12-sided polygon to that of the hexagon is $\dfrac {12a}6 = 4 \cos 30^\circ \tan 15^\circ \approx \boxed{0.928}$ .