This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
37 solutions
hey man, if u join BO so the angles OEB=OBE=30 thus make the angle BOE will equal 120 , but according to your image, the angle BOE is an acute angle so I don't know how u found the solution
Log in to reply
never think an angle acute,obtuse or right by just lookng and guessing
frankly i too faced this same problem. though 30 has been deemed as the right ans i think that the angle value is wrong
Log in to reply
this was the the problem i faced while giving my pre-boards exam ....teachers in school dont even think that students generally visualize the problems an pre-solve it inside there head.....but i am happy to see that people on this globe are like me....:D
althought it 's easy but it take some time with me but at the end i solved it
good way to learn maths
Log in to reply
It was the question that I got in my high school pre-board's mathematics exam .....and I was like ....shit man this just rocked my head.
the x and y taken by you are different, please solve it again
(y)
it is this same way i solved...
30
use radius as equal side n sum of angles in a traingle 180...v vl get dat..
I did in the same way!!
awesome!! I did in the same way!!!!!
but i proved x + y = 165 , please try it out yourself, once again
no no sry..x + y = 150!!! I got it once again! gr8 job!
Something is wrong with this question.
180degrees divided by 3 is30
By drawing a line from B to O, isosceles triangle BOE will be formed. That gives angle BOE = 180-2(30)=120 deg
Angle BOE = Arc BE = 120 deg
Arc CD = 180 deg (semicircle)
The angle formed by two sectors intersecting at the outside of the circle is equal to 1/2 of the difference of the intercepted arcs.
Thus, angle A= 1/2 (Arc CD - Arc BE) = 1/2 (180-120) = 30 deg
interesting , but can you elaborate on, the angle thats formed by 2 sectors a bit more
Based on the principle. The external angle of a cyclic quadrangle is equal to opposite internal angle.
Angle A= (1/2)(measure of arc DC-measure of arc BE) [Angle formed by two intersecting secants] Angle A= (1/2)(180-120) [arc DC is a semicircle; arc BE=angle EOB] Thus, Angle A=(1/2)(60)=30
Cyclic quadrilateral property: If a side of a cyclic quadrilateral is produced then the angle thus formed is equal to the interior opposite angle
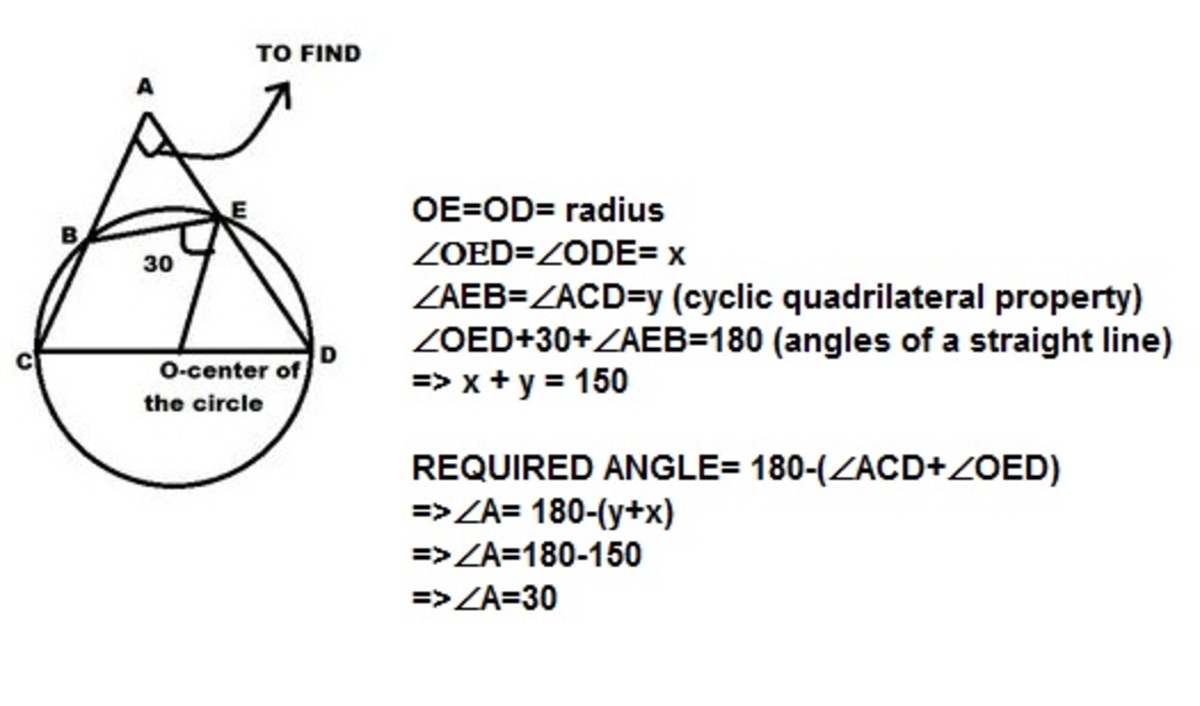 .
.
la parte de arriba no vale jejeje me equivoque =) http://imageshack.com/a/img835/3339/ycfv.jpg
This should be fairly easy this way.
J o i n O B ∠ O B E = 3 0 0 ⇒ ∠ B O E = 1 2 0 0 J o i n C E . N o w ∠ B C E = 6 0 0 ( ∵ ∠ B O E = 1 2 0 0 ) A l s o , ∠ C E A = 9 0 0 ( ∵ ∠ C E D = 9 0 0 , a n g l e i n a s e m i c i r c l e ) N o w , i n Δ C E A , w e h a v e ∠ C = 6 0 0 ∠ E = 9 0 0 ⇒ ∠ A = 3 0 0
itz simple maths i just looked at the triangle and circle if the solvers hav notiesd ,there is a chord BE there is a relation between a chord and the angle next to it
Since O is the center of the circle, <AOD becomes 90º (180-90=90º). E is the center of AD, then <EOD = 45º (90-45=45º). <BEO is 30, then <OED = 60º (90-30=60º). <ODE = 75º [180-(60+45)=75º] <ADC = <ACD, therefore <ADC = 75º and <ACD = 75º <CAD = 30º [180-(75+75)=30º]
good question...bit moderate..but solvable
let a angle @ in ODE triangle.......................... consider big triangle...... u will get the answer
First we join O to B. OE = OB as they are radius of a circle.
Angle EBO = Angle OEB =30 ; angle O = 120 by triangle law .
Then <EOD =<BOC ; OE = OD ; <OED = <ODE =75
So <OED + <OEB + <BEA =180 ; <BEA =75
<BEA = <EBA =75 ; therefore <BAE =30
just let angOED=x
=>angODE= x
=>angAEB= (150-x)
=>angCBE= 180-x ..........(BECD is a cyclic quad, sum of opp angles of a cyclic quad is 180 deg)
=>angABE= 180-(angCBE) =180-(180-x) =x
=>angABE + angAEB + angBAE =180
=>x+(150-x)+angBAE=180
=>angBAE=180-150=30
step one: triangles EOD and ACD are similar as both have the same angel "D", and share the same sides therefore OE is Parallel to CA Step two: in trapezium BCOE , since OE is parallel to CB therefore angle BCO is 30 and angel EOC is 150 Step three: in trapezium ACOE, since OE is parallel to CA and angle EOC equals 30 therefore angle A equals 30
join EC since triangle COE is an isosceles triangle angle CEO=OCE=15; therefore angle COE=150; COD=180 then angle EOD=30 and COB=30. since triagle EOD is also an isosceles triangle so angle OED=ODE 180-EOD=150; OED and ODE equals 150 divide 2 =75 now we had D as 75 angle COB=30 and this is also an isosceles triangle then OCB = OBC; 180-COB=150 ; 150divide 2=75 meaning C=75 C+D+A=180 75+75+A=180 A=180-150= 30
the total angle of a triangle = 180. and from the figure...it is also 30 degrees...
I got the answer just simply rotating OEB counter-clockwise and voila its the same angle with CAD
add the 2 points B& O. after joining these points i got 5 separate triangles (BOC), (BOE),(DOE),(ABE)&(ACD). Now we can consider Triangle (OED), ODE&OED are same angle, i use it as x,from this triangle we get EOD=180-2x. Now we can consider triangle OBE&OEB =30,so BOE=120, then in triangle BOC, B&C is same,we can marked angle B&C as y , by calculating BOC=2x-120. Now at point o, summation of all angles is equal to 180. BOC+BPE+EOD=180. or x+y=150. then at triangle ACD, A+x+y=180or A=30. So, finally in triangle ACD, angle CAD=180-
let the wanted angle is x ,so concider cBED is cyclic quad so x= 180- the sum of angle B and E to know the other steeps contact at [email protected]
steps:
-
join points BO to form triangle BOE(an isosceles triangle)
-
BO = OE;Angle OBE = OEB = 30 deg
-
similarly CO = OD = BO = EO therefore
-
angles BOC = EOD = BEO = 30 deg; angles CBO = OED = (180 - 30)/2 = 75 deg
-
angles ABE = AEB = 180 - (30+75) = 75 ;therefore
angle BAE = 180 - (75+75) = 30 deg....Check
i would like to suggest you to reconsider your 4 point,,,,check it again baby...lol
Draw line BO, angle EBO =30, In quad BECD, 30+CBO+BCD+30+OED+EDC=360, since OED=ODE (angles opposite equal sides of a triangle) similarly BCO=CBO; 2(BCO+CDO)=300 and BCO+CDO= 180-A, 180-A=150 hence A=30.
By drawing a line from B to O - BO is radius and EO aslo radius, Hence <OBE and <OEB are equal i.e <OBE=30. Hence <BOE=120. OC=OB(Radius) so <OCB=<OBC = x OE=OD(Radius) so <ODE=<OED=y Let <COB=k1 and <DOC=k2 Now <COB+<BOE+<DOE=180 ===> k1+k2+120=180===> k1+k2=60 Now x+x+k1=180 and y+y+k2=180 So 2x+2y+k1+k2= 360 ===> 2x+2y=300 ===> x+y=150. Now in Triangle ACD x+y+<A = 180 ===> <A=30
join BO &angles OCB=OBC=y(OC & OB are radius) similarly angles OED=ODE=x(OE & OD are radius) similarly angles OBE=OEB=30(OE & OB are radius) CBED is a cyclic quardilatral- Therefore, CBE+CDE=180 (cyclic quardilatral property) (y+30)+x=180 , x+y=150 we know that BCD=x & ODE=y Therefore , BCD+ODE+CAD=180, x+y+CAD=180 150+CAD=180 (x+y=150,proved above ) CAD=180-150 =30
Let us join BO. Now,angle OBE = angle OEB = 30 .Similarly,angle Ode= angle oed.angle OCB= angle OBC.y+30+x=180 x+y=150.So,angle A = 30 x is angle deo is x and cbo is y. bedc is cyclic so, b+d and e+c is 180
ok
what are x and y?
x is angle deo and angle cbo is y. bedc is cyclic so, b+d and e+c is 180
Let angle OED=X, angle ODE=angle OED(base angles of an isosceles triangle) ,CBED is a cyclic Quad. BCD+BED=180, BCD+30+x=180, BCD=150-x, In triangle CAD, 150-x+x+CAD=180, CAD=180-150, CAD=30 Ans.
itz very easy join the CE now let suppose radius of circle be R then CD=2R & CE=R now apply sin rule angle CDE=90 now ....... sinCED/CD=sinCDE/CE SIN90/2R=SINCDE/R sinCDE=1/2 angle CDE=30 degree
Easy just using that all the angles of triangle are 180 and by isoscales rule its directly comes that A = 30
let <acd = X , <adc = y
in triangle abe and triangle adc
angle X = angle aeb (angle acd + angle deb = 180 , and also angle deb + angle aeb )
similarly , angle adc = Y = angle abe (angle adc + angle cbe = 180 and also angle ceb + angle abe = 180)
so, triangle abc is similar to triangle adc
also,
angle obc=angle ocb = X ( isosceles triangle )
angle ode = angle oed = Y ( isosceles triangle )
also , angle obe = 30 degree ,
we know , angle X + 30 drgree + angle Y = 180 degree ( opposite angle of a cyclic quadrilateral )
similarly, angle Y + 30 degree + angle X = 180 degree( opposite angle of a cyclic quadrilateral )
so , angle X + angle Y = 150 degree
also , in triangle , ABE , angle ABE + angle AEB + angle BAE = 180 degree
X + Y + angle BAE = 180
or, but , X + Y = 150 degree
so angle BAE= 30 degree
join BO &angles OCB=OBC=y(OC & OB are radius) similarly angles OED=ODE=x(OE & OD are radius) similarly angles OBE=OEB=30(OE & OB are radius) CBED is a cyclic quardilatral- Therefore, CBE+CDE=180 (cyclic quardilatral property) (y+30)+x=180 x+y=150 we know that BCD=x & ODE=y Therefore , BCD+ODE+CAD=180 x+y+CAD=180 150+CAD=180 (x+y=150,proved above ) CAD=180-150 =30
In the triangle EOD- EO = OD[radii of the. same circle] now this gives»»»» ang.OED = ang.ODE[ang. opp. to eql sides] let »»» ang.OED=(x)=ang.OD---(1) we know... BCDE is a cyclic quadrilateral.... Thus.... ang.BCD+ang.BED=180° ang.BCD+ang. BEO +ang. OED =180 ang. BCD+30+x =180....[by (1)) and given] Now- ang.BCD =180-30-x =150-x---(2) Now- In tri.ACD--- ang.ACD+ang.ADC+ang.CAD=180 Now.. (150-x)+(x)+CAD=180 -x and+x cancelled out to give- CAD +150=180 CAD= 180-150 =30°
angle ODE = angle OED (angles opp. to equal sides) = x angle CBE = 180 - x (opp. angles of cyclc quad.) angle BEA = 150 - x (linear pair with ang. BED = 30 +x ) now, angle BAE = 180 - (x + 150 - x ) = 30 (angle sum prop.)
Join points CE,we find trangle x COE issocellaes trianle where anles OCE &CEO are 15 degree leaving angle COE=150 degree,accordingly angleEOD+30 degree. Again anles ODE and angle OED =75 degree each,From anle BEO which is 30 degree ( given),we get anleBEA 75 degree and finally angle BAE _ 30 degree ANS
K.K.GARG,INDIA
DEO is an equilateral triangel so each angle degrees = 60. angle BEA=180-angle DEO-angle BEO= 180-60-30=90 angle EBA is different line angle of BEO so the degrees is 60 So the angle CAD = angle BAE = 180-angle BEA-angle EBA = 180-90-60= 30
how can you say that triangle DEO is an equilateral triangle?
Why triangle DEO Is An Equilateral triangle?
DEO is an equilateral triangle?
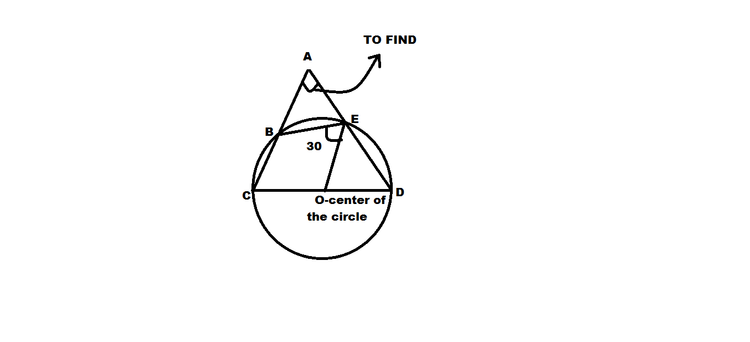
join BO &angles OCB=OBC=y(OC & OB are radius) similarly angles OED=ODE=x(OE & OD are radius) similarly angles OBE=OEB=30(OE & OB are radius) CBED is a cyclic quardilatral- Therefore, CBE+CDE=180 (cyclic quardilatral property) (y+30)+x=180 x+y=150 we know that BCD=x & ODE=y Therefore , BCD+ODE+CAD=180 x+y+CAD=180 150+CAD=180 (x+y=150,proved above ) CAD=180-150 =30