Rectangles Squared
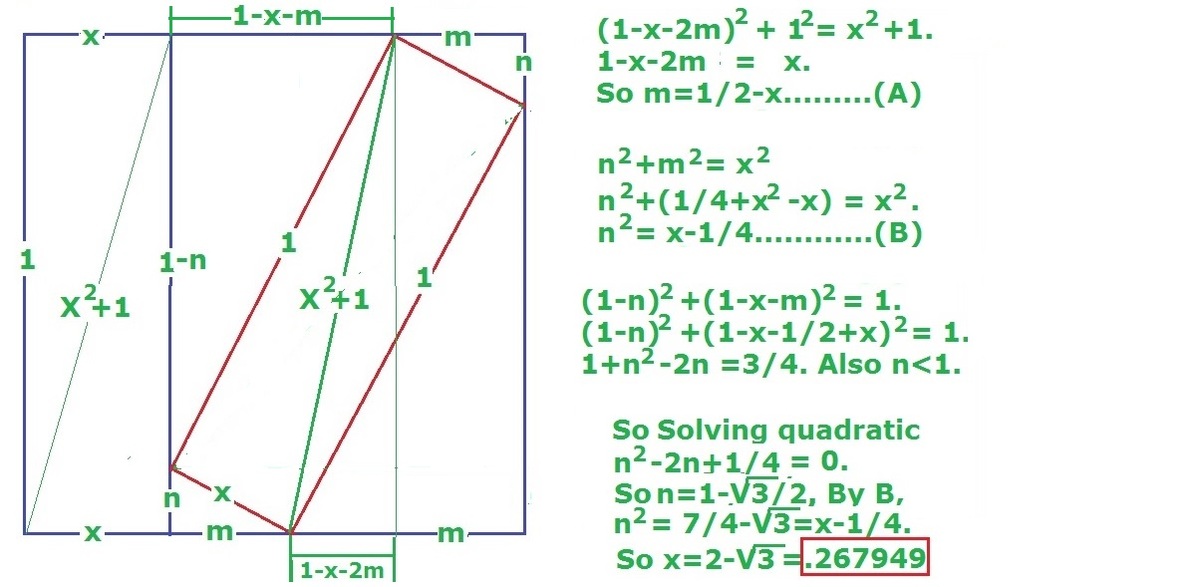
Two congruent rectangles of dimensions 1 × x are placed inside a square of side length 1. One of them is vertical, and the other is inclined.
Find the side length x to 3 decimal places.
The answer is 0.267.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice problem and solution. One typo to point out; I think that you meant that cos ( θ ) = 2 1 , giving us θ = 3 π radians.
Nice simple solution. up voted. I post my solution just as another solution. Not a better one.
It would be interesting to know how you solved the equations. I would do it as under.
x
C
o
s
θ
+
S
i
n
θ
=
1
.
.
.
.
.
.
.
.
.
.
.
.
.
(
A
)
x
+
x
S
i
n
θ
+
C
o
s
θ
=
1
.
.
.
.
.
.
.
.
.
(
B
)
F
r
o
m
(
A
)
x
=
C
o
s
θ
1
−
S
i
n
θ
F
r
o
m
(
B
)
x
=
1
+
S
i
n
θ
1
−
C
o
s
θ
∴
(
1
−
S
i
n
θ
)
(
1
+
S
i
n
θ
)
=
C
o
s
θ
(
1
−
C
o
s
θ
)
∴
C
o
s
2
θ
=
C
o
s
θ
(
1
−
C
o
s
θ
)
,
C
o
s
θ
=
0
.
⟹
C
o
s
θ
=
1
−
C
o
s
θ
.
⟹
C
o
s
θ
=
2
1
.
Let θ be the angle of inclination relative to the horizontal of the second rectangle.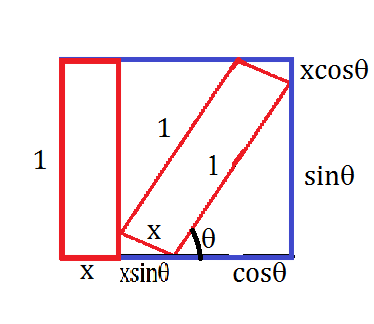
From that we have that the sides of the square become
x
cos
θ
+
sin
θ
and
x
+
x
sin
θ
+
cos
θ
which constitute a system of equations because we have the side of the square,
x
cos
θ
+
sin
θ
=
1
x
+
x
sin
θ
+
cos
θ
=
1
Solving it would lead to
cos
θ
=
2
1
and
x
=
2
−
3
, using three decimal places the answer is
2
−
1
,
7
3
2
0
5
0
8
0
7
=
0
.
2
6
7