A geometry problem by Vivek Vijayan
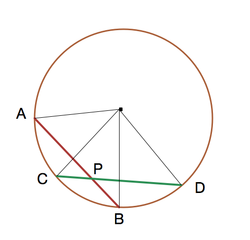 Two chords AB and CD of circle with center O, meet at the point P such that
∠
A
O
C
=
5
0
o
,
∠
B
O
D
=
4
0
o
.
What is the acute angle between lines
A
B
and
C
D
?
Two chords AB and CD of circle with center O, meet at the point P such that
∠
A
O
C
=
5
0
o
,
∠
B
O
D
=
4
0
o
.
What is the acute angle between lines
A
B
and
C
D
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You can just deduct 135 degrees from 180 degrees since it's a supplementary angle.
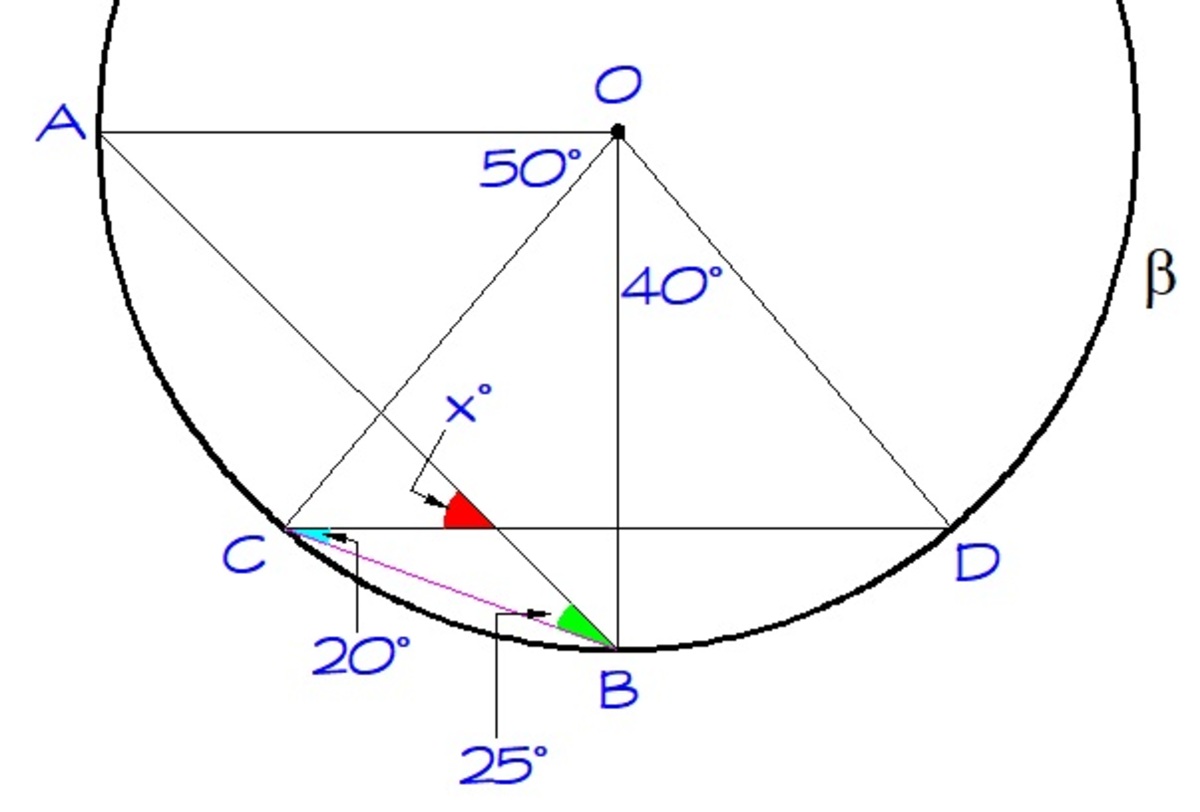
By the inscribed angle theorem, we have
∠ D C B = 2 1 ( 4 0 ) = 2 0 ∘
∠ A B C = 2 1 ( 5 0 ) = 2 5 ∘
By the exterior angle theorem, we have
x = 2 0 + 2 5 = 4 5
Draw the side BC, now, ∠ B O D = 4 0 o g i v e s ∠ B C D = 2 0 o and ∠ A O C = 5 0 o g i v e s ∠ A B C = 2 5 o
This gives ∠ B P C = 1 8 0 − ( 2 0 + 2 5 ) = 1 3 5 o Hence the acute angle between the chords is ( 3 6 0 − ( 1 3 5 × 2 ) ) ÷ 2 = 4 5 o