A geometry problem by well max

I visualised it this way (apologies, the letters on the diagrams are unclear)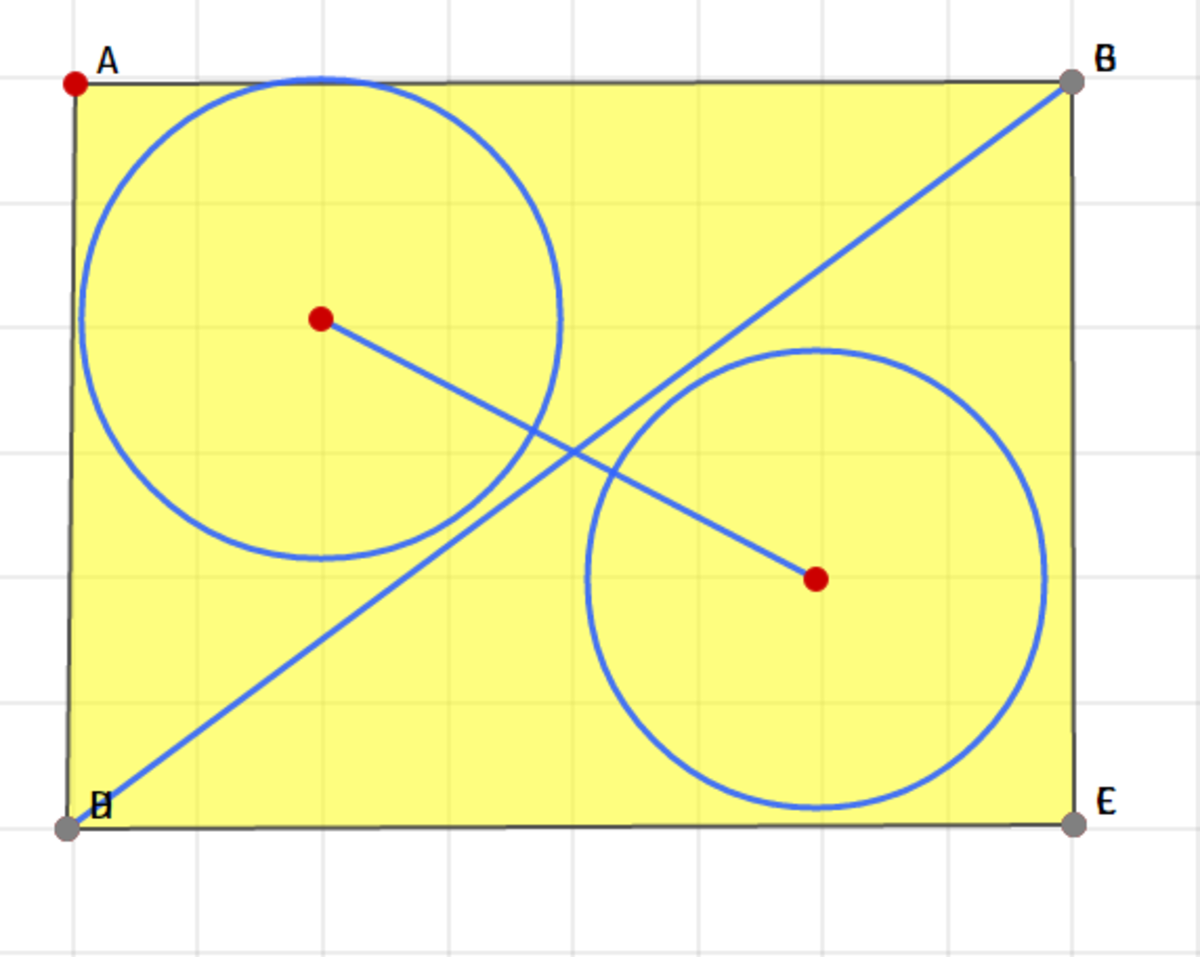 You can find the radius of an incircle with the formula $\frac { 2a }{ p }$ where $a$ is the area of the triangle and $p$ is the perimeter. This works out to be $\frac { 12 }{ 12 } =1$ .

By my roughly drawn lines, you can see that a right triangle can be formed, using the knowledge of lengths AB, BC and the circles' radii. Now it's just a case of Pythag, ${ 1 }^{ 2 }+{ 2 }^{ 2 }={ x }^{ 2 }$

${ x }^{ 2 }=\boxed { 5 }$

To find the radius of inscribed circle O, we use the area relationship K = rs, where r is the in-radius and s is the semi-perimeter. Triangle ABD is a 3-4-5 right triangle, with area 3*4/2 = 6. Applying gives r = 1.

Place ABCD in a coordinate grid with D(0, 0), A(0, 3), B(4, 3), and C(4, 0). Knowing that circles O and P are inscribed in congruent triangles, we know they must be congruent, too. Because r = 1, drawing in the tangents from O to AB and AD gives O as (1, 2). Similarly, we can reason out P as (3, 1). Applying the distance formula gives $x^{2}$ = $2^{2}$ + $1^{2}$ = $5$ .