A geometry problem by Wildan Bagus Wicaksono

Geometry Level 1

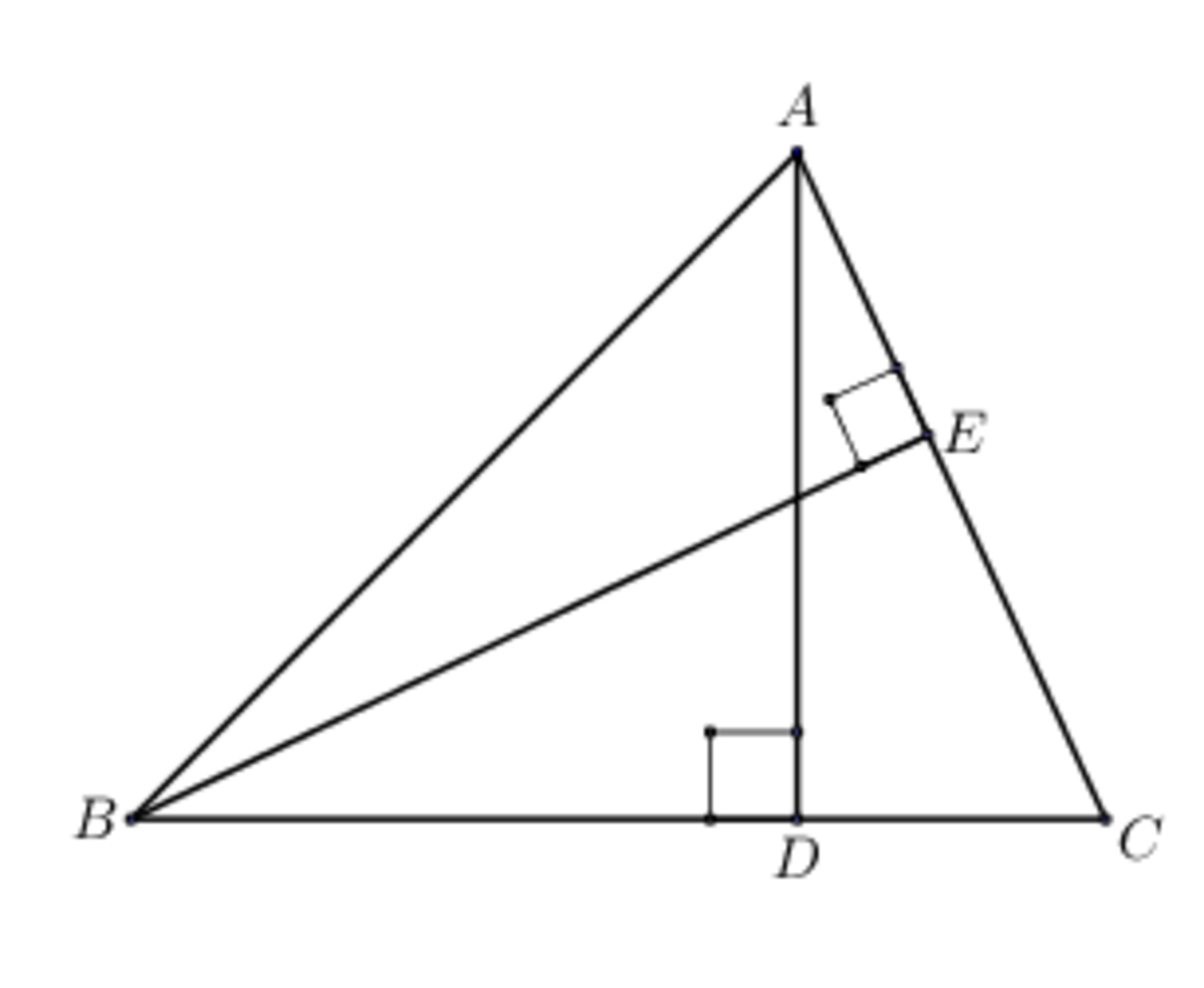
Given the △ A B C \triangle ABC . The lines A D AD and B E BE are each perpendicular to the sides B C BC and A C AC and intersect at point H H . Find the value

( A H ⋅ H D B H ⋅ H E ) 10 { \left( \frac { AH\cdot HD }{ BH\cdot HE } \right) }^{ 10 }


The answer is 1.

Wildan Bagus Wicaksono by Wildan Bagus Wicaksono , 18, Indonesia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

See the picture above. △ A H E \triangle AHE opposite to △ B H D \triangle BHD means ∠ A H E = ∠ B H D \angle AHE=\angle BHD . ∠ A E H = ∠ B D H = 90 \angle AEH=\angle BDH=90 and ∠ E A H = ∠ D B H \angle EAH=\angle DBH . This means that △ A H E \triangle AHE is similar to △ D B H \triangle DBH . Based on equivalent comparisons on two similar triangles:

A H B H = H E H D \frac { AH }{ BH } =\frac { HE }{ HD } or A H ⋅ H D = B H ⋅ H E AH\cdot HD=BH\cdot HE .

So, ( A H ⋅ H D B H ⋅ H E ) 10 = 1 10 = 1 { \left( \frac { AH\cdot HD }{ BH\cdot HE } \right) }^{ 10 }={ 1 }^{ 10 }=\boxed { 1 } .

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...