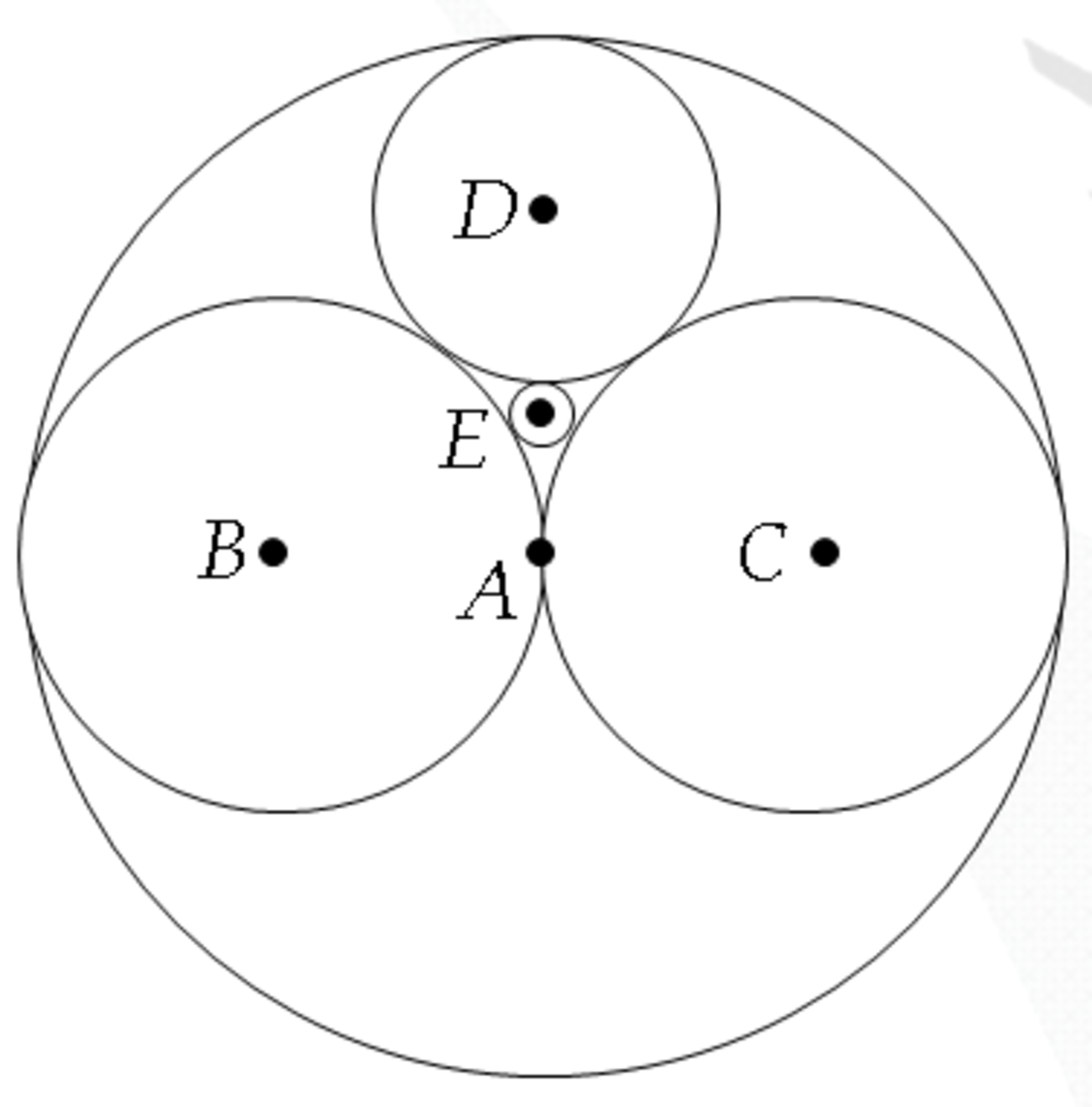
A geometry problem by Wildan Bagus Wicaksono

Geometry Level 2

Circles $B$ and $C$ are congruently placed inside so that both offend the arc of circle $A$ . The centers of circles $A$ , $B$ , and $C$ lie in line. Circle $D$ alludes to the arc of circles $A$ , $B$ , and $C$ . Circle $E$ alludes to the circles $B$ , $C$ , and $D$ . Determine the ratio of radius of circle $E$ to radius of circle $A$ .

2 : 15 1 : 15 3 : 17 2 : 7

2 solutions

Marta Reece
Jun 22, 2017

Let radius of circle $A$ be $1$ , radius of circle $D$ be $R$ , and radius of circle $E$ be $r$ .

$\triangle ACD$ in a right triangle and $\left(\frac12\right)^2+\left(1-R\right)^2=\left(\frac12+R\right)^2$

The solution is $R=\frac13$

In $\triangle ACE$ similarly $\left(\frac12\right)^2+\left(1-2R-r\right)^2=\left(\frac12+r\right)^2$

Using the fact that $R=\frac13$ , solution is $r=\boxed{\frac1{15}}$

Sahil Bansal
Jun 22, 2017

1:15 is the ratio of radius of circle E to radius of circle A. Just correct that in your question.

Sorry, I am not careful Thank you for the criticism.

Wildan Bagus Wicaksono - 3 years, 11 months ago

Can you edit the problem to update this error? You can do so by selecting "Edit problem" from the menu.

Calvin Lin Staff - 3 years, 11 months ago

Can explain where the menu is?

Wildan Bagus Wicaksono - 3 years, 11 months ago

I see that you've managed to update the problem :)

For reference, problem writers are able to edit and delete their own problem by clicking on the "dot dot dot" menu. On desktop, this is what it looks like:

Calvin Lin Staff - 3 years, 11 months ago

A geometry problem by Wildan Bagus Wicaksono

2 solutions

0 pending reports