Double Popsicle
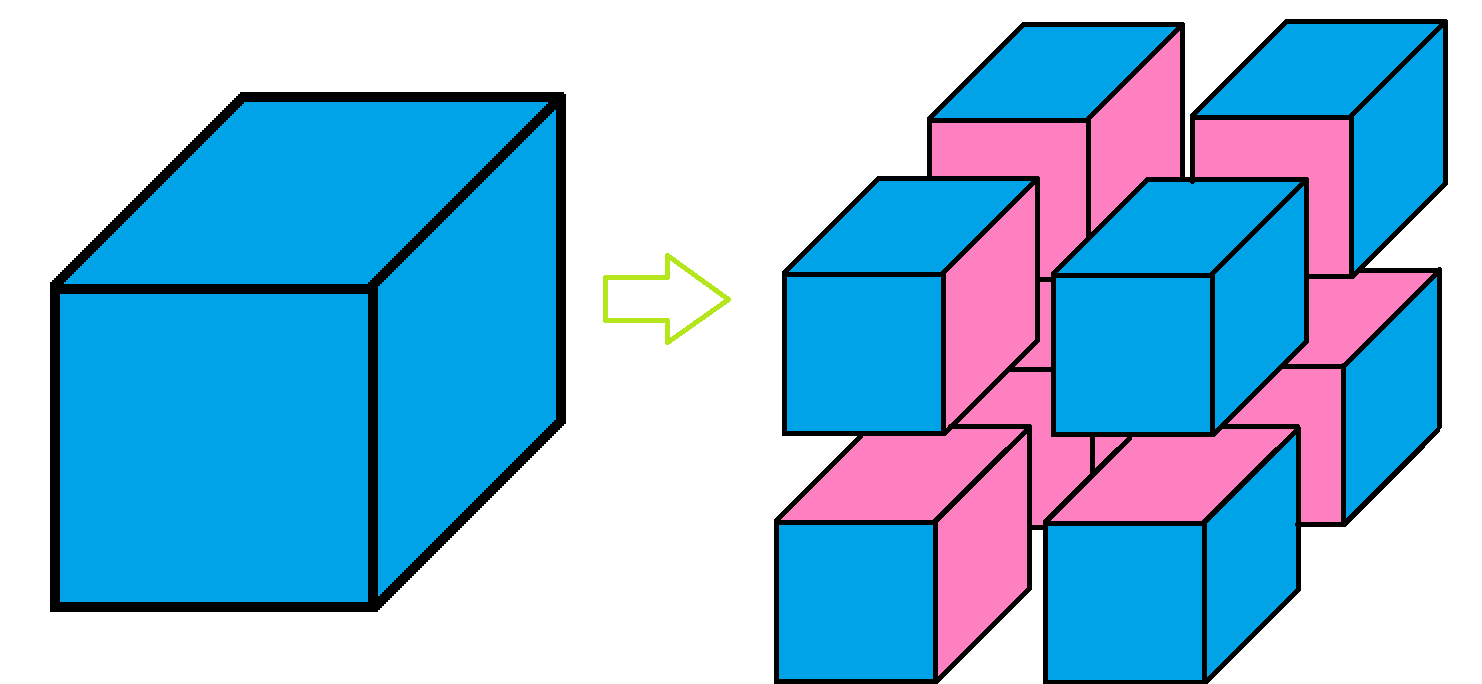
A pink strawberry-flavored cubic popsicle is coated with blue blueberry-flavored icing.
If the popsicle cube is divided into 8 smaller cubes of equal size, which color will have more surface area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Simple and elegant solution!
Relevant wiki: Surface Area of a Cuboid
Let S be the side length of the big popsicle cube.
Then the total blue surface area = 6 S 2
Now for each smaller cube, the total surface area of each small cube = 6 ( 2 S ) 2 = 2 3 S 2 .
Hence, the total surface area of all 8 small cubes = 8 × 2 3 S 2 = 1 2 S 2 .
In other words, the total surface is doubled after the symmetrical division.
Therefore, the pink surface area = total colored surface area - blue surface area = 1 2 S 2 − 6 S 2 = 6 S 2 .
As a result, the pink and blue surfaces have the same area.
Moderator note:
There's a simpler solution.
Hint : Did you notice that each of 8 smaller cubes are a different orientation to each other?
Thank you. I know. Just thought algebraic proof is easier to understood.
While you could write out the formulas, the much easier method is to simply look for symmetries and count.
Each of the 8 cuboids are identical. To see why, rotate or flip the entire cube in any direction and you'll see the symmetry.
We therefore only need to check the surface area of a single cuboid. Three faces are blue, three faces are pink. Therefore, both surface areas are equal.
By direct counting, there are 24 blue faces (3 on each smaller cube). There are also 24 pink faces (3 on each smaller cube).
Um, my solution is more visual...
A cube has 6 sides.
If you were to cut (this tasty cube) in half, you'd get (for one cube) 1 pink and 5 blue sides.
Cut that in half, you'd get 2 pink and 4 blue sides (we have 4 cubes total now)
Cut that in half, and you have 3 pink and 3 blue sides and 8 cubes total.
Since we have cubes and they each have the same number of pink and blue, you can say the surface area is the same.
The initial cube had 6 large blue sides.When you divide it, each large face turns into 4 smaller blue sides. Therefore we have 24 blue sides.
The total number of sides of the 8 smaller cubes is 48. Therefore the number of pink sides is 48-24=24.
Since the number of identically-sized blue sides and pink sides is the same, the surface area is the same.