A geometry problem by Yahia El Haw
Geometry
Level
3
The two circles below have equal radii of 4 units each and the distance between their centers is 6 units. Find the area of the shaded region to 2 decimal places.
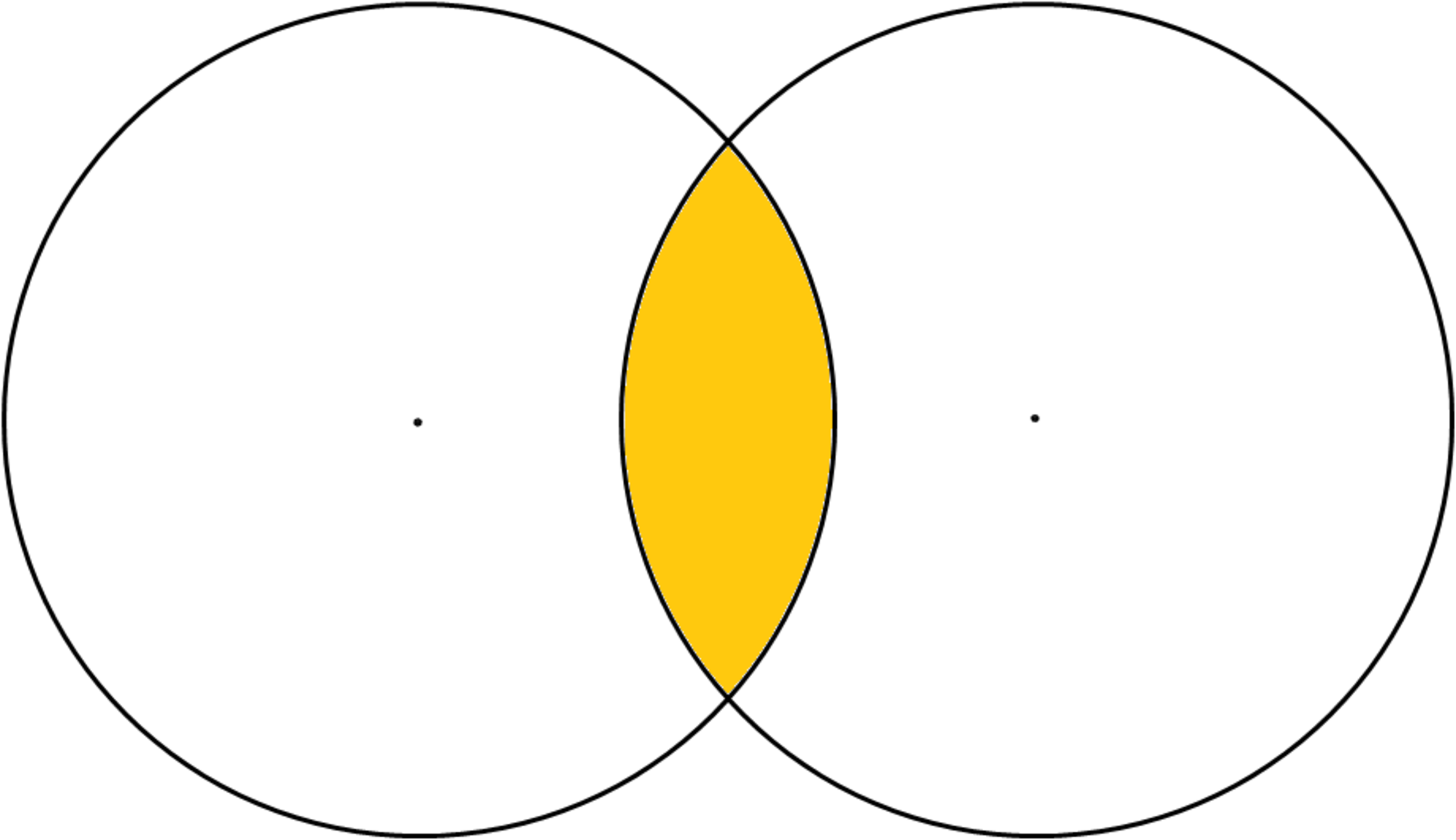
The answer is 7.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A . Because of symmetry, the shaded region may be considered as made up of two equal (in area) regions. The area of the left half of the shaded region is given by the area of the sector BOC minus the area of the triangle BOC.
B . ength of OM = 3 (by symmetry) since distance between centers is 6, and radius r = 4.
C . Let t be the measure of angle BOM.
D . cos(t) = OM/OB = 3/4 , t = arccos(3/4) : using right triangle BOM.
E . area of sector BOC = (1/2)(2t)r2
F . area of triangle BOC = (1/2)sin(2t)r2
G . area of shaded region = 2 [ (1/2)(2t)r2 - (1/2)sin(2t)r2 ]
H . = [2t - sin(2t)] r2 = 7.25 square units (rounded to 3 decimal places)